Section:
Research Program
Probabilistic and symbolic dynamics
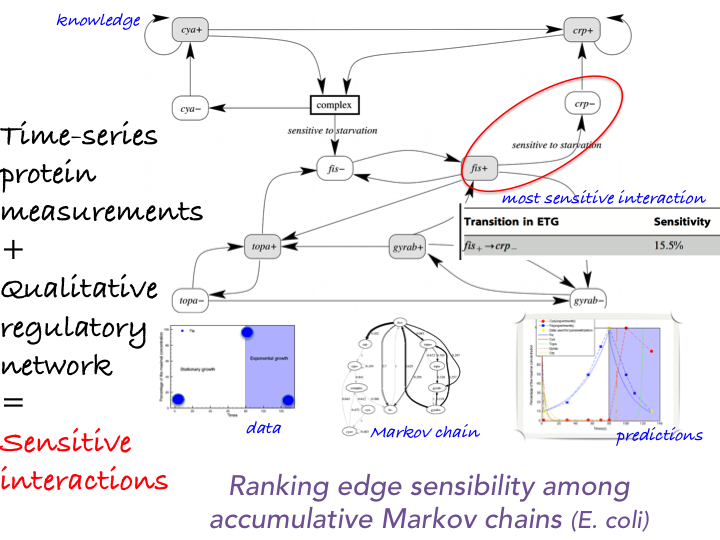
We work on new techniques to emphasize biological strategies that must occur to reproduce quantitative measurements in order to predict the quantitative response of a system at a larger-scale. Our framework mixes mechanistic and probabilistic modeling [1] . The system is modeled by an Event Transition Graph, that is, a Markovian qualitative description of its dynamics together with quantitative laws which describe the effect of the dynamic transitions over higher scale quantitative measurements. Then, a few time-series quantitative measurements are provided. Following an ergodic assumption and average case analysis properties, we know that a multiplicative accumulation law on a Markov chain asymptotically follows a log-normal law with explicit parameters [52] . This property can be derived into constraints to describe the set of admissible weighted Markov chains whose asymptotic behavior agrees with the quantitative measures at hand. A precise study
of this constrained space via local search optimization emphasizes the most important discrete events that must occur to reproduce the information at hand. These methods have been validated on the E. coli regulatory network benchmark. See Figure 2 for illustration.
We now plan to apply these techniques to reduced networks representing the main pathways and actors automatically generated from the integrative methods developed in the former section.
This requires to improve the range of dynamics that can be modeled by these techniques, as well as the efficiency and scalability of the local search algorithms.
Figure
2.
Prediction of the quantitative behavior of a system using average-case analysis of dynamical systems and identification of key interactions [1] .
Input data are provided by a qualitative description of the system dynamics at the transcription level (interaction graph) and 3 concentration measurements of the protein (population scale). The method computes an Event-Transition Graph. Interaction frequencies required to predict the population scale behavior as the asymptotic behavior of an accumulation multiplicative law over a Markov chain. Estimation by local searches in the space of Markov chains consistent with the observed dynamics and whose asymptotic behavior is consistent with quantitative observations at the population scale. Edge thickness reflects their sensitivity in the search space.
It allows to predict the protein concentration (red curve) which fits with observations.
Additionally, literature evidences that high sensitivity ETG transitions correspond to
key interaction in E. Coli response to nutritional stress.
|
|