Section: New Results
User-centered Models for Shapes
Our goal, is to develop responsive shape models, i.e. 3D models that respond in the expected way under any user action, by maintaining specific application-dependent constraints (such as a volumetric objects keeping their volume when bent, or cloth-like surfaces remaining developable during deformation, etc). We are extending this approach to composite objects made of distributions and/or combination of sub-shapes of various dimensions.
Implicit modeling
Participants : Antoine Bégault, Marie-Paule Cani, Michael Gleicher, Cédric Zanni.
|
Our insight towards 3D shapes that respond in an intuitive way during both design and animation is to develop representations that clearly separate changes of structure - namely, the morphology of the shape - from changes of posture (its current 3D isometric embedding). Using skeletons is an excellent way to do so for 3D solids: the structure of a shape is represented by the topology of the skeleton, the length of its components and the shape thickness around it, while the shape posture is defined by the embedding of the skeleton in 3D space. Implicit surfaces (iso-surfaces of scalar fields) are the best mathematical model so far for generating 3D shapes from skeletons. However, a number of long standing problems - blending at distance that makes topology unpredictable, bulges at junctions, blurring of details - reduced the interest for this representation for many years. We addressed several of these issues in the last few years. Our most recent contribution is a method for enabling topology control in the case n-ary implicit blends [17] . Shapes are modeled using scale-invariant integral primitives (SCALIS) along skeletons, and blend with a plus. We use field warping to avoid unwanted blending and provide a unique control (based for instance on the angle) on the way skeleton-based primitives are allowed to blend. See Figure 4
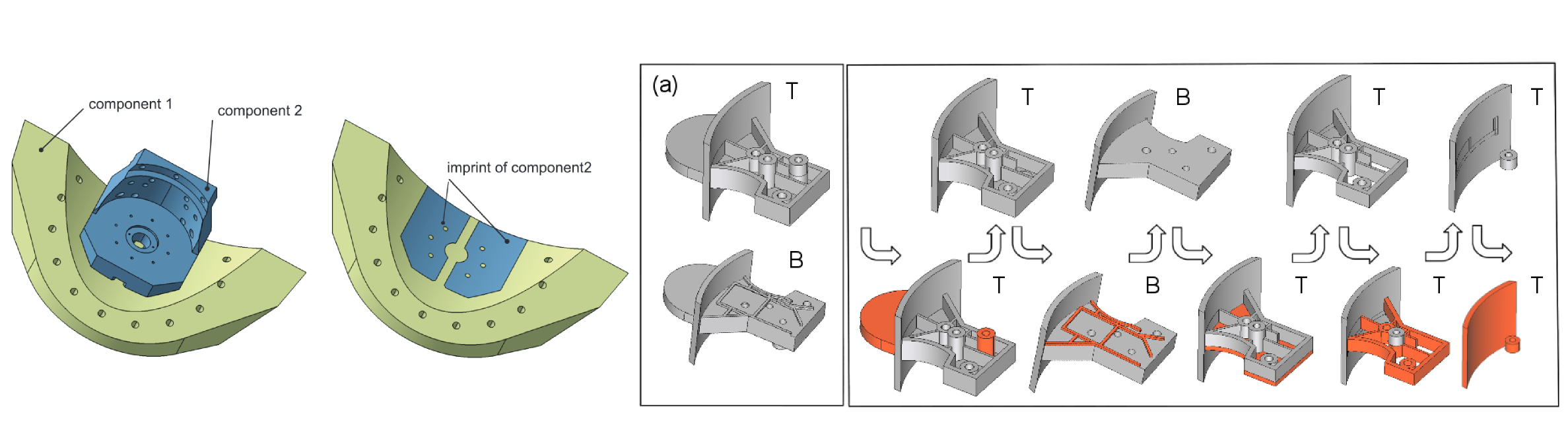
Towards responsive assemblies
Participants : Stefanie Hahmann, Jean-Claude Léon, Aarohi Singh Johal.
|
We chose to focus on man-made objects to tackle the topic of shape assemblies, since CAD models of virtual industrial prototypes provide an excellent, real-size test-bed for our methods. Moreover, this is perfectly fitting the demand from industrial partners such as Airbus group and EDF.
Assemblies representing products are most often reduced to a collection of independent CAD models representing each component. The designation of each component and information about its function are often missing. As a result, geometric interfaces between components are unknown. These interfaces are particularly useful for structural mechanics to be able to quickly generate a Finite Element model of the assembly. This is especially critical when the latter gets very complex. [8] addresses the problem of automatically generating a class of geometric interfaces for very complex assemblies. GPU-based algorithms have proved suitable to obtain reliable results on CAD models.
Precisely determining interfaces between components is also a first requirement to enrich geometric models with functional information, since a subset of functions derives from interfaces between components. Based on both geometric interfaces and on a new concept of conventional interfaces, we proposed a series of approaches [13] , [3] that make use of qualitative and ontology-based reasoning to connect CAD components and their geometric interfaces to functions or to functional designations of components: this results into an intrinsic identifier of a component in an assembly that connects it to its function.
To efficiently process assemblies of components, shape analysis [40] is particularly useful to generate the dimensionally reduced models needed for structural mechanics. [2] shows that analyzing a B-Rep CAD model to derive a construction graph, i.e. a set of construction trees, can be a robust basis to generate dimensionally reduced models.
Lastly, we extended shape analysis methods to detect some sets of symmetries [9] . Recovering this knowledge and embedding it into a model is the first step towards functionality-preserving deformations of complex man-made prototypes.
Parametric shapes
Participants : Stefanie Hahmann, Léo Allemand-Giorgis, Tibor Stanko.
|
We are developing new smooth parametric surface models defined on irregular quad meshes. They are in fact a powerful alternative to subdivision surface and singularly parameterized tensor product surfaces since they combine the advantages of both, the arbitrary topology of quad meshes and the smoothness of the tensor product patches. In collaboration with G.-P. Bonneau (Maverick team) several parametric triangular surface models for arbitrary topologies have been developed in the past. A new surface spline model has been published [1] and presented at GMP’14. It solves the problem of defining a G-continuous surface interpolating the vertices of an arbitrary quad mesh with low degree polynomial tensor product patches. It further aims to produce shapes of very high visual quality while reducing the number of control points, see Figure 6(right).
Another contribution concerns the modeling and smoothing of shapes using the Morse-Smale complex. The Morse-Smale complex is a topological structure defined on scalar functions which extracts critical points of the function and the links between them. By encoding a hierarchy between critical points, less important critical points can be deleted in order to simplify the structure. Our goal is to reconstruct a new shape, which corresponds to the simplified structure while approximating the initial data and preserving the most salient features. We first developed a method for interpolating monotone increasing 2D scalar data with a monotone piecewise cubic C-continuous surface. Monotonicity is a sufficient condition for a function to be free of critical points inside its domain. We overcome the restrictive standard axial monotonicity for tensor-product surfaces and introduce sufficient conditions and two algorithms for a more relaxed monotonicity constraint [38] , see a piecewise monotonic shape in Figure 6(left). Then, some preliminary results on shape reconstruction from Morse-Smale complexes have been presented as a Posterand at a national conference [35] .
In collaboration with Hans Hagen and Anne Berres from University of Kaiserslautern, we investigated conditions under which shape deformations preserve surface curvatures. The work has been published as a chapiter in a scientific book [39] .