Section: New Results

Visualization

Participants : Léo Allemand-Giorgis, Georges-Pierre Bonneau [contact] .

In computer visualization we have worked on two topics: topology for visualization and perception for visualization.

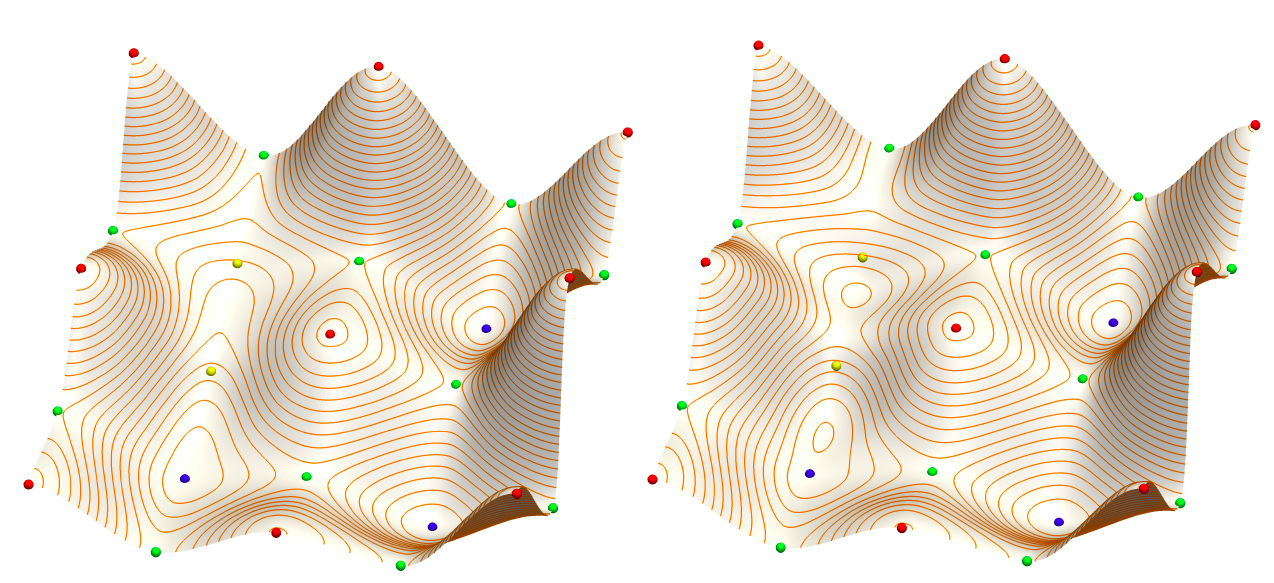
In topology for visualization we have worked on scalar field vizualization methods taking into account the topology of the data. In [15] We have derived theoretical results on monotonic interpolation of scalar data. Our method enables to interpolate given topological data such as minima, maxima and saddle points at the corners of a rectangular domain without adding spurious extrema inside the function domain, as illustrated in Figure 7 .

We have collaborated to a state of the art chapter on Uncertain Visualization [16] , in which we described the evaluation of visualization methods based on visual perception.

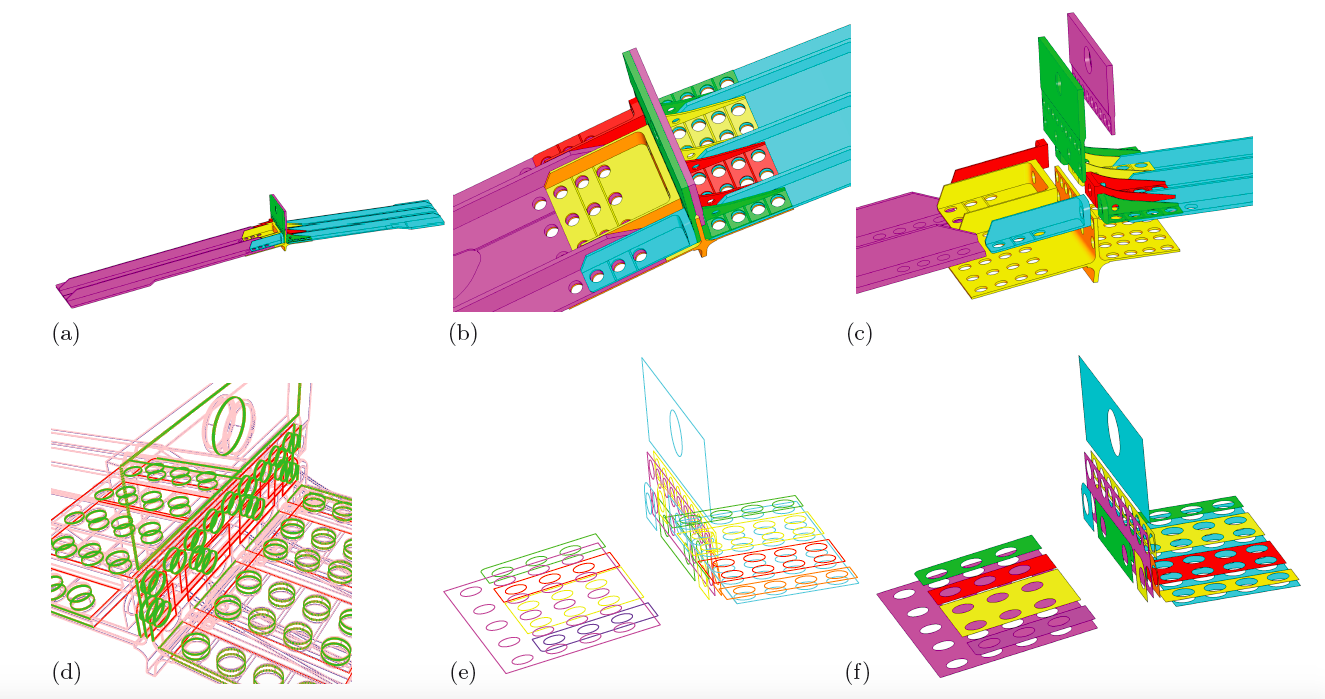
Furthermore we have worked on two topics related to geometry for visualization. In [6] we introduce a method for interpolating a quad mesh using G1-continuous polynomial surfaces. We plan to use this method in the future for displaying isosurfaces of higher order data. In [12] we have published a method for reconstructing interfaces in highly complex assemblies, as illustrated in Figure 8 . This method has been developed in order to visualize data arising from simulation of complex mechanical assemblies, within the ANR project ROMMA, closed in January 2014.