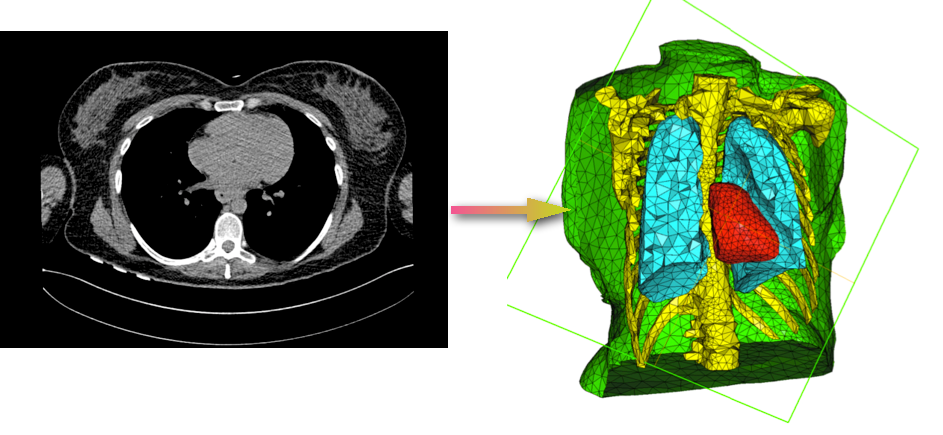
Section: New Results

Inverse Problem

Electrocardiograms simulated by our group with a highly realistic and detailed forward model were used for several inverse-modeling studies [34] , [33] , [38] , [35] .

• Stability analysis of the POD reduced order method for solving the bidomain model in cardiac electrophysiology: In this work we show the numerical stability of the Proper Orthogonal Decomposition (POD) reduced order method used in cardiac electrophysiology applications. The difficulty of proving the stability comes from the fact that we are interested in the bidomain model, which is a system of degenerate parabolic equations coupled to a system of ODEs representing the cell membrane electrical activity. The proof of the stability of this method is based an a priori estimate controlling the gap between the reduced order solution and the Galerkin finite element one. We present some numerical simulations confirming the theoretical results. We also combine the POD method with a time splitting scheme allowing a faster solution of the bidomain problem and show numerical results. Finally, we conduct numerical simulation in 2D illustrating the stability of the POD method in its sensitivity to the ionic model parameters. We also perform 3D simulation using a massively parallel code. We show the computational gain using the POD reduced order model. We also show that this method has a better scalability than the full finite element method.

• In silico assessment of drugs effects on human embryonic stem cells derived cardiomyocytes electrical activity: Computational modeling and simulation is extensively used to investigate diseases in cardiac electrophysiological activity and also drug effects, side effects and interactions. Human embryonic stem cell-derived cardiomyocytes (hESC-CMs) have been recently considered as a promising tool in regenerative medicine: their major role in repairing damaged tissue is due to pluripotency and ability to differentiate. These pluripotent cells are also used in early stages of drugs development. Pharmaceutical companies use the MultiElectrode Array (MEA) device in order to perform many in vitro experiments on hESC-CMs. The goal of our study is to derive a mathematical model and to simulate these in vitro experiments.

• Sensitivity of the Electrocardiography Inverse Solution to the Torso Conductivity Uncertainties: Electrocardiography imaging (ECGI) is a new non invasive technology used for heart diagnosis. It allows to construct the electrical potential on the heart surface only from measurement on the body surface and some geometrical informations of the torso. The purpose of this work is twofold: First, we propose a new formulation to calculate the distribution of the electric potential on the heart, from measurements on the torso surface. Second, we study the influence of the errors and uncertainties on the conductivity parameters, on the ECGI solution. We use an optimal control formulation for the mathematical formulation of the problem with a stochastic diffusion equation as a constraint. The descretization is done using stochastic Galerkin method allowing to separate random and de-terministic variables. The optimal control problem is solved using a conjugate gradient method where the gradient of the cost function is computed with an ad-joint technique. The efficiency of this approach to solve the inverse problem and the usability to quantify the effect of conductivity uncertainties in the torso are demonstrated through a number of numerical simulations on a 2D geometrical model. Our results show that adding $\pm 50\%$ uncertainties in the fat conductivity does not alter the inverse solution, whereas adding $\pm 50\%$ uncertainties in the lung conductivity affects the reconstructed heart potential by almost $50\%$.

• Inverse Localization of Ischemia in a 3D Realistic Geometry: A Level Set Approach: The reconstruction of cardiac ischemic regions from body surface potential measurements (BSPMs) is usually performed at a single time instant which corresponds to the plateau or resting phase of the cardiac action potential. Using a different approach, we previously proposed a level set formulation that incorporates the knowledge of the cardiac excitation process in the inverse procedure, thus exploiting the spatio-temporal correlations contained in the BSPMs. In this study, we extend our inverse level-set formulation for the reconstruction of ischemic regions to 3D realistic geometries, and analyze its performance in different noisy scenarios. Our method is benchmarked against zero-order Tikhonov regularization. The inverse reconstruction of the ischemic region is evaluated using the correlation coefficient (CC), the sensitive error ratio (SN), and the specificity error ratio (SP). Our algorithm outperforms zero-order Tikhonov regularization, specially in highly noisy scenarios.

• Inverse problem in electrocardography via the factorization method of boundary value problems: We present a new mathematical approach for solving the inverse problem in electrocardiography. This approach is based on the factorization of boundary value problems method. In this paper we derive the mathematical equations and test this method on synthetical data generated on realistic heart and torso geometries using the state-of-the-art bidomain model in the heart coupled to the Laplace equation in the torso. We measure the accuracy of the inverse solution using spatial Relative Error (RE) and Correlation Coefficient (CC).

• In the inverse problem en electrocardiology, the goal is to recover electrophysiological activity in the heart without measuring directly on its surface (without using catheter in- terventions). Note that today the inverse computation is frequently used by solving the quasi-static model. This model doesn’t take into account the heart dynamic in time and may result in considerable errors in the reconstruction of the solution on the heart. In [1] we study a 3D numerical inverse problem constrained by the bidomain equations in electro- cardiology. The state equations consisting in a coupled reaction-di↵usion system modelling the propagation of the intracelullar and extracellular electrical potentials, and ionic cur- rents, are extended to further consider the e↵ect of an external bathing medium. Thus, we demonstrate that the novel concept of applying electrophysiological data might be useful to improve noninvasive reconstruction of electrical heart activity. Finally, we present numerical experiments representing the e↵ect of the heart dynamic on the inverse solutions. Moreover in [2], we study the stability result for the conductivities of the approximate bidomain model. The proof is based on the combination of a Carleman estimate obtained in [3] and certain weight energy estimates for parabolic systems.

• The static inverse ECG problem needs to solve the well known ill posed Cauchy problem for the Laplace equation. A new approach investigated in the team uses the method of factorization of bounadary value problems. This method, studied for itself, provides in this context the com- putation of Dirichlet-Neumann operators as solution of a Riccati equation. Results have been presented at IEEE international symposium on biomedical imaging, New York april 16-19, 2015. Further investigations will be lead using more precise numerical methods to solve the Riccati equation. The non-linearity and time dependence of the coupling resistance between cardiac cells (gap junctions) is stdied in the Liryc institute and thought to be of importance in the unerstanding of cardiac arrhythmias. The internship of Nhan Le Thanh was a first step to investigate their numerical simulation.

An Example of calculus on a torso is shown in figure 1

Figure 1. Mesh of the torso obtained with an IRM picture; this problem is link with the IDAM project