Section: New Results

An Efficient Volumetric Framework for Shape Tracking

Recovering 3D shape motion using visual information is an important problem with many applications in computer vision and computer graphics, among other domains. Most existing approaches rely on surface-based strategies, where surface models are fit to visual surface observations. While numerically plausible, this paradigm ignores the fact that the observed surfaces often delimit volumetric shapes, for which deformations are constrained by the volume inside the shape. Consequently, surface-based strategies can fail when the observations define several feasible surfaces, whereas volumetric considerations are more restrictive with respect to the admissible solutions. In this work, we investigate a novel volumetric shape parametrization to track shapes over temporal sequences. In constrast to Eulerian grid discretizations of the observation space, such as voxels, we consider general shape tesselations yielding more convenient cell decompositions, in particular the Centroidal Voronoi Tesselation. With this shape representation, we devise a tracking method that exploits volumetric information, both for the data term evaluating observation conformity, and for expressing deformation constraints that enforce prior assumptions on motion. Experiments on several datasets demonstrate similar or improved precisions over state-of-the-art methods, as well as improved robustness, a critical issue when tracking sequentially over time frames. This work was accepted as oral at CVPR 2015 (less than 3% acceptance rate) [8] .

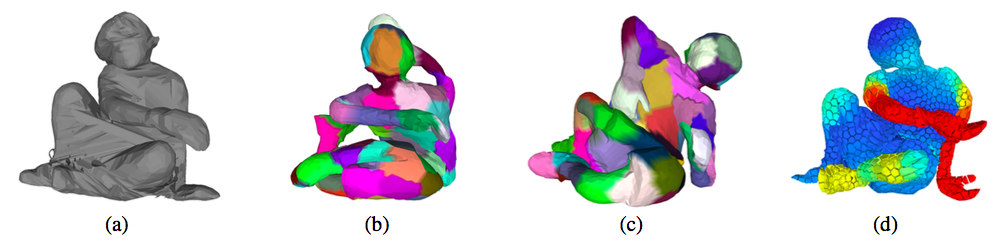
Figure 4. Frames of the goalkeeper dataset acquired on the Kinovis platform. (a) Visual hull input. (b) Tracking result of Cagniart et al. 2010. (c) Allain et al. 2014. (d) This method [8] . Note the improved angular shapes and the improved robustness.