Section: Research Program

Hardware-efficient quantum information processing

In this scientific program, we will explore various theoretical and experimental issues concerning protection and manipulation of quantum information. Indeed, the next, critical stage in the development of Quantum Information Processing (QIP) is most certainly the active quantum error correction (QEC). Through this stage one designs, possibly using many physical qubits, an encoded logical qubit which is protected against major decoherence channels and hence admits a significantly longer effective coherence time than a physical qubit. Reliable (fault-tolerant) computation with protected logical qubits usually comes at the expense of a significant overhead in the hardware (up to thousands of physical qubits per logical qubit). Each of the involved physical qubits still needs to satisfy the best achievable properties (coherence times, coupling strengths and tunability). More remarkably, one needs to avoid undesired interactions between various subsystems. This is going to be a major difficulty for qubits on a single chip.

The usual approach for the realization of QEC is to use many qubits to obtain a larger Hilbert space of the qubit register  [113] , [117] . By redundantly encoding quantum information in this Hilbert space of larger dimension one make the QEC tractable: different error channels lead to distinguishable error syndromes. There are two major drawbacks in using multi-qubit registers. The first, fundamental, drawback is that with each added physical qubit, several new decoherence channels are added. Because of the exponential increase of the Hilbert's space dimension versus the linear increase in the number of decay channels, using enough qubits, one is able to eventually protect quantum information against decoherence. However, multiplying the number of possible errors, this requires measuring more error syndromes. Note furthermore that, in general, some of these new decoherence channels can lead to correlated action on many qubits and this needs to be taken into account with extra care: in particular, such kind of non-local error channels are problematic for surface codes. The second, more practical, drawback is that it is still extremely challenging to build a register of more than on the order of 10 qubits where each of the qubits is required to satisfy near the best achieved properties: these properties include the coherence time, the coupling strengths and the tunability. Indeed, building such a register is not merely only a fabrication task but rather, one requirers to look for architectures such that, each individual qubit can be addressed and controlled independently from the others. One is also required to make sure that all the noise channels are well-controlled and uncorrelated for the QEC to be effective.

We have recently introduced a new paradigm for encoding and protecting quantum information in a quantum harmonic oscillator (e.g. a high-Q mode of a 3D superconducting cavity) instead of a multi-qubit register  [84] . The infinite dimensional Hilbert space of such a system can be used to redundantly encode quantum information. The power of this idea lies in the fact that the dominant decoherence channel in a cavity is photon damping, and no more decay channels are added if we increase the number of photons we insert in the cavity. Hence, only a single error syndrome needs to be measured to identify if an error has occurred or not. Indeed, we are convinced that most early proposals on continuous variable QIP  [78] , [70] could be revisited taking into account the design flexibilities of Quantum Superconducting Circuits (QSC) and the new coupling regimes that are provided by these systems. In particular, we have illustrated that coupling a qubit to the cavity mode in the strong dispersive regime provides an important controllability over the Hilbert space of the cavity mode  [83] . Through a recent experimental work [10] , we benefit from this controllability to prepare superpositions of quasi-orthogonal coherent states, also known as Schrödinger cat states.

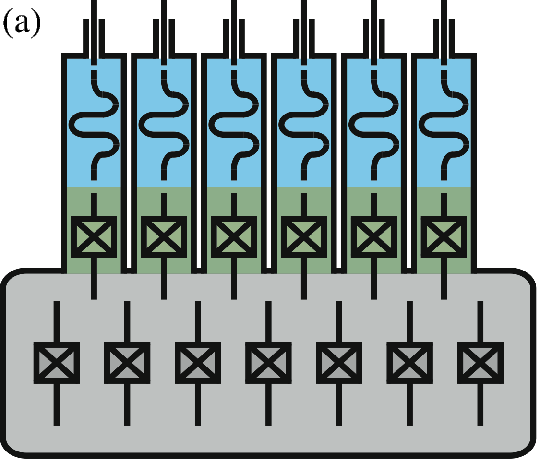
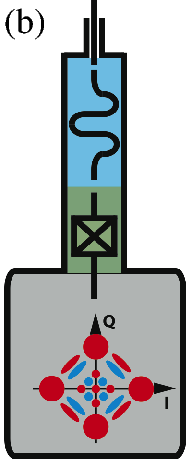
In this Scheme, the logical qubit is encoded in a four-component Schrödinger cat state. Continuous quantum non-demolition (QND) monitoring of a single physical observable, consisting of photon number parity, enables then the tractability of single photon jumps. We obtain therefore a first-order quantum error correcting code using only a single high-Q cavity mode (for the storage of quantum information), a single qubit (providing the non-linearity needed for controllability) and a single low-Q cavity mode (for reading out the error syndrome). As shown in Figure 2 , this leads to a significant hardware economy for realization of a protected logical qubit. Our goal here is to push these ideas towards a reliable and hardware-efficient paradigm for universal quantum computation.

Figure 2. (a) A protected logical qubit consisting of a register of many qubits: here, we see a possible architecture for the Steane code  [117] consisting of 7 qubits requiring the measurement of 6 error syndromes. In this sketch, 7 transmon qubits in a high-Q resonator and the measurement of the 6 error syndromes is ensured through 6 additional ancillary qubits with the possibility of individual readout of the ancillary qubits via independent low-Q resonators. (b) Minimal architecture for a protected logical qubit, adapted to circuit quantum electrodynamics experiments. Quantum information is encoded in a Schrödinger cat state of a single high-Q resonator mode and a single error syndrome is measured, using a single ancillary transmon qubit and the associated readout low-Q resonator.