Section: Research Program

Reduced kinetic models for plasmas

As already said, kinetic plasmas computer simulations are very intensive, because of the gyrokinetic turbulence. In some situations, it is possible to make assumptions on the shape of the distribution function that simplify the model. We obtain in this way a family of fluid or reduced models.

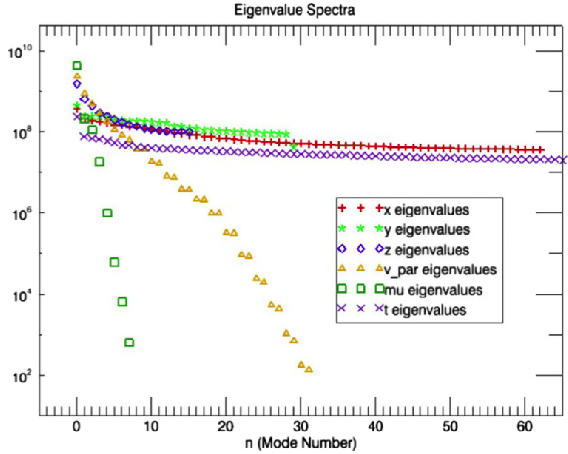
Assuming that the distribution function has a Maxwellian shape, for instance, we obtain the MagnetoHydroDynamic (MHD) model. It is physically valid only in some parts of the tokamak (at the edges for instance). The fluid model is generally obtained from the hypothesis that the collisions between particles are strong. Fine collision models are mainly investigated by other partners of the IPL (Inria Project Lab) FRATRES. In our approach we do not assume that the collisions are strong, but rather try to adapt the representation of the distribution function according to its shape, keeping the kinetic effects. The reduction is not necessarily a consequence of collisional effects. Indeed, even without collisions, the plasma may still relax to an equilibrium state over sufficiently long time scales (Landau damping effect). Recently, a team at the Plasma Physics Institut (IPP) in Garching has carried out a statistical analysis of the 5D distribution functions obtained from gyrokinetic tokamak simulations [32] . They discovered that the fluctuations are much higher in the space directions than in the velocity directions (see Figure 1 ).

This indicates that the approximation of the distribution function could require fewer data while still achieving a good representation, even in the collisionless regime.

Our approach is different from the fluid approximation. In what follows we call this the “reduced model” approach. A reduced model is a model where the explicit dependency on the velocity variable is removed. In a more mathematical way, we consider that in some regions of the plasma, it is possible to exhibit a (preferably small) set of parameters $\alpha$ that allows us to describe the main properties of the plasma with a generalized “Maxwellian” $M$. Then

In this case it is sufficient to solve for $\alpha (x,t)$. Generally, the vector $\alpha$ is solution of a first order hyperbolic system.

Several approaches are possible: waterbag approximations, velocity space transforms, etc.

Velocity space transformations

An experiment made in the 60's [35] exhibits in a spectacular way the reversible nature of the Vlasov equations. When two perturbations are applied to a plasma at different times, at first the plasma seems to damp and reach an equilibrium. But the information of the perturbations is still here and “hidden” in the high frequency microscopic oscillations of the distribution function. At a later time a resonance occurs and the plasma produces an echo. The time at which the echo occurs can be computed (see Villani (Landau damping. CEMRACS 2010 lectures. http://smai.emath.fr/cemracs/cemracs10/PROJ/Villani-lectures.pdf ), page 74). The fine mathematical study of this phenomenon allowed C. Villani and C. Mouhot to prove their famous result on the rigorous nonlinear Landau damping [37] .

More practically, this experiment and its theoretical framework show that it is interesting to represent the distribution function by an expansion on an orthonormal basis of oscillating functions in the velocity variables. This representation allows a better control of the energy transfer between the low frequencies and the high frequencies in the velocity direction, and thus provides more relevant numerical methods. This kind of approach is studied for instance by Eliasson in [29] with the Fourier expansion.

In long time scales, filamentation phenomena result in high frequency oscillations in velocity space that numerical schemes cannot resolve. For stability purposes, most numerical schemes contain dissipation mechanisms that may affect the precision of the finest oscillations that could be resolved.

Adaptive modeling

Another trend in scientific computing is to optimize the computation time through adaptive modeling. This approach consists in applying the more efficient model locally, in the computational domain, according to an error indicator. In tokamak simulations, this kind of approach could be very efficient, if we are able to choose locally the best intermediate kinetic-fluid model as the computation runs. This field of research is very promising. It requires developing a clever hierarchy of models, rigorous error indicators, versatile software architecture, and algorithms adapted to new multicore computers.

Numerical schemes

As previously indicated, an efficient method for solving the reduced models is the Discontinuous Galerkin (DG) approach. It is possible to make it of arbitrary order. It requires limiters when it is applied to nonlinear PDEs occurring for instance in fluid mechanics. But the reduced models that we intent to write are essentially linear. The nonlinearity is concentrated in a few coupling source terms.

In addition, this method, when written in a special set of variables, called the entropy variables, has nice properties concerning the entropy dissipation of the model. It opens the door to constructing numerical schemes with good conservation properties and no entropy dissipation, as already used for other systems of PDEs [39] , [25] , [34] , [33] .