Section: New Results

Cancer

Participants : Luis Lopes Neves de Almeida, Group Emmanuel Barillot [Institut Curie] , Catherine Bonnet [DISCO team, Saclay] , Thibault Bourgeron, Group Kai Breuhahn [Hospital of University of Heidelberg, Pathology] , Rebecca Chisholm, Jean Clairambault, François Delhommeau [Haematology department, St Antoine Hospital, Paris] , Marie Doumic, Dirk Drasdo, Walid Djema [DISCO team, Saclay] , Julie Favre [EPFL, Lausanne] , Olivier Fercoq [Télécom ParisTech] , Ghassen Haddad [ENIT, Tunis] , Shalla Hanson [Department of mathematics, Duke University, Durham, NC] , Pierre Hirsch [Haematology department, St Antoine Hospital, Paris] , Groups Invade, Lungsysii, Hicham Janati [ENSAE, Paris] , Tim Johann, Group Klingmueller [German Cancer Center, Heidelberg] , Michal Kowalczyk [Univ. Santiago de Chile] , Annette Larsen [Cancer biology and therapeutics lab, St Antoine Hospital, Paris] , Tommaso Lorenzi [University of St Andrews, Scotland] , Alexander Lorz, Frédéric Mazenc [DISCO team, Saclay] , Benoît Perthame, Camille Pouchol, Andrada Quillas Maran, Fernando Quirós [Univ. Autónoma de Madrid] , Michèle Sabbah [Cancer biology and therapeutics lab, St Antoine Hospital, Paris] , Min Tang [Jiaotong University, Shanghai] , Teresa Teixeira [IBCP] , Emmanuel Trélat [LJLL, UPMC] , Paul Van Liedekerke, Oliver Sedlaczek [German Cancer Center (DKFZ) and Hospital of University of Heidelberg, Germany] , François Vallette [INSERM, CRCNA, Nantes] , Nicolas Vauchelet, Irène Vignon-Clementel [REO] , Zhou Xu [IBCP] , Yi Yin.

Senescence and telomere shortening

In many animals, aging tissues accumulate senescent cells, a process which underlies the loss of regeneration capacity of organs and is ultimately detrimental to the organism. Senescence is also required to protect organisms from unlimited proliferation that may arise from numerous stimuli or deregulations. Due to these opposing effects in aging and cancer, senescence is considered antagonistic pleiotropic; senescence is beneficial to protect from cancer in the young organism, but becomes detrimental late in life. Therefore, understanding the mechanisms of cellular senescence may lead to the development of global therapies to debilities specific for the aged, as well age-associated diseases and cancer. These are major public health issues in France, and other western aging countries.

Replicative senescence, induced by telomere shortening, exhibits considerable asynchrony and heterogeneity, the origins of which remain unclear. In [19], following  [61], we formally study how telomere shortening mechanisms impact on senescence kinetics and define two regimes of senescence, depending on the initial telomere length variance. We provide analytical solutions to the model, highlighting a non-linear relationship between senescence onset and initial telomere length distribution. This study reveals the complexity of the collective behaviour of telomeres as they shorten, leading to senescence heterogeneity.

Stability analysis of a delay differential model of healthy and leukaemic haematopoiesis

The collaboration with the DISCO team (Inria Saclay, C. Bonnet, F. Mazenc and their PhD student W. Djema), supported by the collaboration with the team of haematologists led by F. Delhommeau at St. Antoine Hospital in Paris, has been continued, with common research work underway. A new model describing the coexistence between ordinary and mutated haematopoietic stem cells was introduced and analysed in [32]. Interpreting theoretical conditions found to guarantee the survival of healthy cells while eradicating unhealthy ones leads us to propose possibly innovative therapies obtained by combining the infusion of different drugs (Flt-3 inhibitors such as quizartinib, cytosine arabinoside, anthracyclines).

Interactions between tumour cell populations and their cellular micro-environments

This is the main object of study, together with the consideration of phenotype and genotype heterogeneity in cancer cell populations (see Highlights of the Year), of the THE ITMO Cancer national call 2016, to which two (out of three) of the submitted projects involving our team, which themselves were two out of the six laureate projects at the national level, have been successfully funded. The two projects, EcoAML and MoGlImaging have been launched in November 2016.

Evolution and cancer; drug resistance in cancer cell populations

We have continued to develop our phenotypically based models of drug-induced drug resistance in cancer cell populations, representing their Darwinian or Lamarckian evolution under drug pressure by integro-differential equations. The properties of phenotype-structured PDEs are explored in theoretical articles with examples [25], [78]. We will also use them in the two projects laureates to the THE (Tumour Heterogeneity in its Ecosystem) ITMO Cancer call of 2016 (see Highlights of the Year), EcoAML and MoGlImaging, to help predict early evolution towards leukaemogenesis (EcoAML, leader F. Delhommeau, St. Antoine Hospital, Paris) and emergence of resistance to temozolomide in glioblastoma cell populations (MoGlImaging, leader E. Moyal, Toulouse, F. Vallette, Nantes, being our main work correspondent). In this version, mutualistic exchanges between the cancer cell population and its supporting stroma will be represented as impinging on the phenotypic variables that describe the relevant heterogeneity at stake in the two cell populations.

With F.  Vallette, we have co-supervised Hicham Janati's ENSAE 2nd year (M1) internship on the investigation of cancer resistance in a Glioblastoma cell line [46] with gene expression data coming from F. Vallette's lab in Nantes. This internship represents for us a first step in the quest for relevant (most likely multidimensional) phenotypes, based on bioinformatic and biostatistic methods to process experimental dynamic gene expression data, to interactively identify our physiologically structured models of heterogeneity and its evolution in cancer cell populations. The task ahead is immense, but our commitment in the THE consortium (see Highlights of the Year) with biologists providing us with such data (F. Vallette, F. Delhommeau) gives us good expectations to be successful with it in a close future. Following Hicham Janati's internship [46], Julie Favre (M1 student at EPFL) has been hired in a new internship to set the practical grounds for the interactive collaboration (begun with the THE program in November 2016) between our team and F. Delhommeau's team on model-based processing of gene expression data produced by a heterogeneous leukaemic cell population and by its surrounding stromal cell population.

The evolution towards drug-induced drug resistance in cancer cell populations may be described by methods of adaptive dynamics for continuous phenotype-structured populations, as such cell populations are fundamentally phenotypically, if not genetically, heterogeneous. In [11], [40], we review the bases of heterogeneity and drug resistance in cancer, its assessment by biological experiments and by mathematical modelling and methods of optimal control that may be applied to represent and optimise combined delivery of cytotoxic and cytostatic drugs, see below “Optimal control and drug resistance” [52].

Therapy optimisation

PK-PD: optimisation with respect to unwanted side effects. A previous pharmacokinetics-pharmacodynamics (PK-PD) model for the action of anticancer drugs at the molecular level, coupled with an age-structured linear model of the cell division cycle, has been updated in [12] (introduced in a special issue on PK-PD [9]) with optimisation of the combined delivery of 3 different drugs (5-fluorouracil, oxaliplatin, leucovorin). This is joint work with Olivier Fercoq, Télécom ParisTech. It represents the coalescence of two distinct types of models, both studied in previous years in our team: molecular ODE-based models of the action of anticancer drugs, and optimisation (using a Uzawa-like algorithm applied to the first eigenvalues of the two growing populations, minimising the cancer eigenvalue - objective - while maintaining the healthy eigenvalue above a reference threshold - constraint -, supposed to be linked to the state of health of the patient) of the control of linear growth models based on age-structured transport equations for the cell division cycle in the two populations separately.

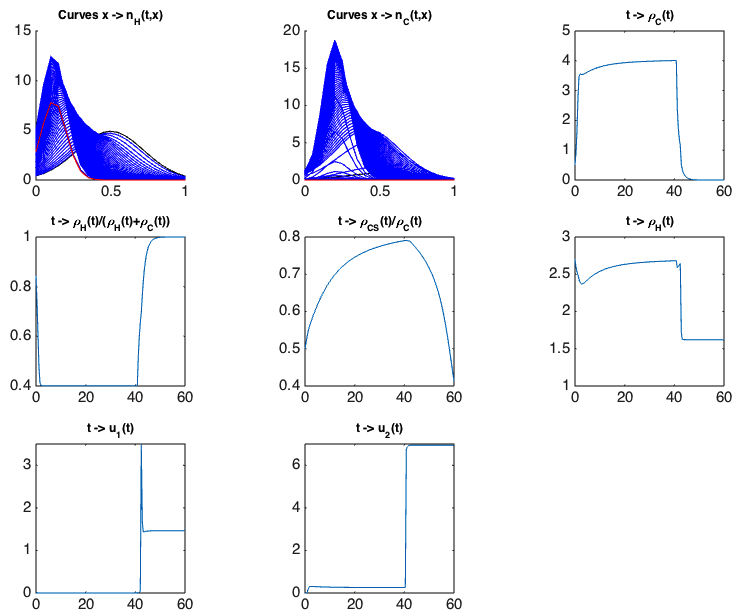
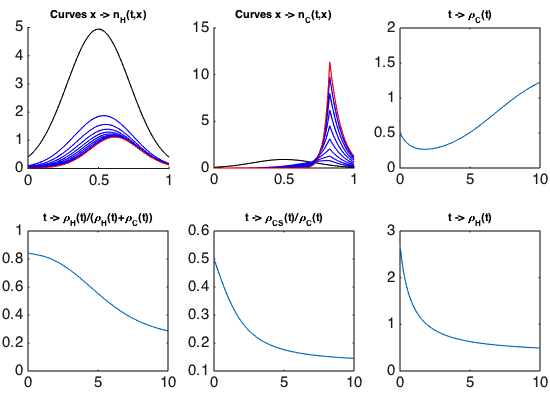
Optimal control and drug resistance. In the framework of Camille Pouchol's PhD thesis, co-supervised at LJLL by E. Trélat and J. Clairambault, analysing the behaviour of healthy and cancer cell populations structured in a continuous resistance phenotype to a cytotoxic drug, and exposed to cytostatic and cytotoxic chemotherapies, we have firstly established, in an asymptotic analysis using a Lyapunov functional inspired from works by P.-E. Jabin and G. Raoul  [77], results of convergence and concentration for constant drug concentrations [52] (following  [84]). In a second part of this work, we have derived from them analytical conditions of optimality for the delivery of the drugs in a general class of controls. A numerical example of the optimal strategy is illustrated on Figure 1, where the phenotype $x$ continuously ranges from totally sensitive ($x=0$) to totally resistant ($x=1$), and healthy and cancer cells are represented by densities of cells $n_H(t,x)$, $n_C(t,x)$. The simulations confirm that the optimal strategy consists of letting the cancer cell population become more and more homogeneous around a sensitive phenotype, and then to use the maximal amount of drugs. This proposed strategy may be related with the “drug holiday” practiced in the clinic of cancers. We also show en passant the clearly detrimental effect of delivering cytotoxic drugs at high constant doses, as they inevitably induce the emergence of a thriving resistant subpopulation, which is illustrated on Figure 2.

Lung and breast cancer

Diffusion-weighted magnetic resonance imaging (DWI) is a key non-invasive imaging technique for cancer diagnosis and tumour treatment assessment, reflecting Brownian movement of water molecules in tissues. Since densely packed cells restrict molecule mobility, tumour tissues produce less attenuated DWI signals than normal tissues. However, no general quantitative relation between DWI data and the cell density has been established. In order to link low-resolution clinical cross-sectional data with high-resolution histological information, we have developed an image processing and analysis chain, which was used to study the correlation between the diffusion coefficient (D value) estimated from DWI and tumour cellularity from serial histological slides of a resected non-small cell lung cancer (NSCLC) tumour. Colour deconvolution followed by cell nuclei segmentation was performed on digitised histological images to determine local and cell-type specific 2D (two-dimensional) densities. From these the 3D (three-dimensional) cell density was inferred by a model-based sampling technique, which is necessary for the calculation of local and global 3D tumour cell count. Next, DWI sequence information was overlaid with high-resolution CT data and the resected histology using prominent anatomical hallmarks for co-registration of histology tissue blocks and non-invasive imaging modalities for data. The integration of cell numbers information and DWI data derived from different tumour areas revealed a clear negative correlation between cell density and D value. Importantly, spatial tumour density can be quantitatively calculated based on DWI data to estimate tumour heterogeneity [55].

In a followup we currently study to what extent the relation between cellularity and DWI - diffusion coefficient can be inferred from biopsies instead of tumour serial sections. Moreover, we are studying the relation between DWI and tumour microvasculature [33].

Biomechanically mediated growth control of cancer cells

Mechanical feedback has been identified as a key regulator of tissue growth, by which external signals are transduced into a complex intracellular molecular machinery. Using multiscale computational modeling of multicellular growth in two largely different experimental settings with the same tumour cell line we demonstrated that the cellular growth response on external mechanical stress may nevertheless be surprisingly quantitatively predictable. Our computational model represents each cell as an individual unit capable of migration, growth, division, and death and is parameterised by measurable biophysical and bio-kinetic parameters. A cell cycle progression function depending on cell compression was established by comparisons of computer simulations with experiments of spheroids growing in an alginate elastic capsule. After a calibration step with free growing spheroids growing in a liquid suspension to capture the different growth conditions, the model using the same cell cycle progression function can predict the mechanical stress response of spheroid growth in a completely different experimental technique using Dextran, where stress is exerted by osmotic pressure. Our findings suggest that the stress response of cell growth may be highly reproducible even in otherwise different environments. This encourages the idea that robust functional modules may be identified, thus helping us to understand complex cell behaviours such as cell growth and division in relation to mechanical stress. The model analysis further elucidates the relation between applied pressure, cell compressibility and cell density. Moreover, the model developments within this paper points a way of how to handle the so far open issue of high compression within the popular so-called Centre-Based Models, in which force between cells is modelled as forces between cell centres [54].