Section: Research Program
Axis 1: Analysis and Simulation
Challenge: Definition and understanding of phenomena resulting from interactions between light, shape, and matter as seen from an observer point of view.
Results: Theoretical tools and numerical models for analyzing and simulating the observed optical phenomena.
To reach the goals of the MANAO project, we need to increase our understanding of how light, shape, and matter act together in synergy and how the resulting signal is finally observed. For this purpose, we need to identify the different phenomena that may be captured by the targeted observers. This is the main objective of this research axis, and it is achieved by using three approaches: the simulation of interactions between light, shape, and matter, their analysis and the development of new numerical models. This resulting improved knowledge is a foundation for the researches done in the three other axes, and the simulation tools together with the numerical models serve the development of the joint optical/digital systems in Axis 2 and their validation.
One of the main and earliest goals in computer graphics is to faithfully reproduce the real world, focusing mainly on light transport. Compared to researchers in physics, researchers in computer graphics rely on a subset of physical laws (mostly radiative transfer and geometric optics), and their main concern is to efficiently use the limited available computational resources while developing as fast as possible algorithms. For this purpose, a large set of theoretical as well as computational tools has been introduced to take a maximum benefit of hardware specificities. These tools are often dedicated to specific phenomena (e.g., direct or indirect lighting, color bleeding, shadows, caustics). An efficiency-driven approach needs such a classification of light paths [55] in order to develop tailored strategies [101]. For instance, starting from simple direct lighting, more complex phenomena have been progressively introduced: first diffuse indirect illumination [53], [93], then more generic inter-reflections [62], [46] and volumetric scattering [90], [43]. Thanks to this search for efficiency and this classification, researchers in computer graphics have developed a now recognized expertise in fast-simulation of light propagation. Based on finite elements (radiosity techniques) or on unbiased Monte Carlo integration schemes (ray-tracing, particle-tracing, ...), the resulting algorithms and their combination are now sufficiently accurate to be used-back in physical simulations. The MANAO project will continue the search for efficient and accurate simulation techniques, but extending it from computer graphics to optics. Thanks to the close collaboration with scientific researchers from optics, new phenomena beyond radiative transfer and geometric optics will be explored.
Search for algorithmic efficiency and accuracy has to be done in parallel with numerical models. The goal of visual fidelity (generalized to accuracy from an observer point of view in the project) combined with the goal of efficiency leads to the development of alternative representations. For instance, common classical finite-element techniques compute only basis coefficients for each discretization element: the required discretization density would be too large and to computationally expensive to obtain detailed spatial variations and thus visual fidelity. Examples includes texture for decorrelating surface details from surface geometry and high-order wavelets for a multi-scale representation of lighting [42]. The numerical complexity explodes when considering directional properties of light transport such as radiance intensity (Watt per square meter and per steradian - ), reducing the possibility to simulate or accurately represent some optical phenomena. For instance, Haar wavelets have been extended to the spherical domain [92] but are difficult to extend to non-piecewise-constant data [95]. More recently, researches prefer the use of Spherical Radial Basis Functions [98] or Spherical Harmonics [84]. For more complex data, such as reflective properties (e.g., BRDF [77], [63] - 4D), ray-space (e.g., Light-Field [73] - 4D), spatially varying reflective properties (6D - [88]), new models, and representations are still investigated such as rational functions [80] or dedicated models [31] and parameterizations [91], [96]. For each (newly) defined phenomena, we thus explore the space of possible numerical representations to determine the most suited one for a given application, like we have done for BRDF [80].
|
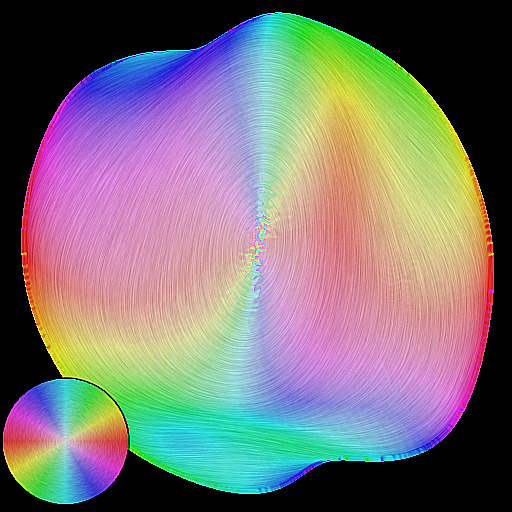
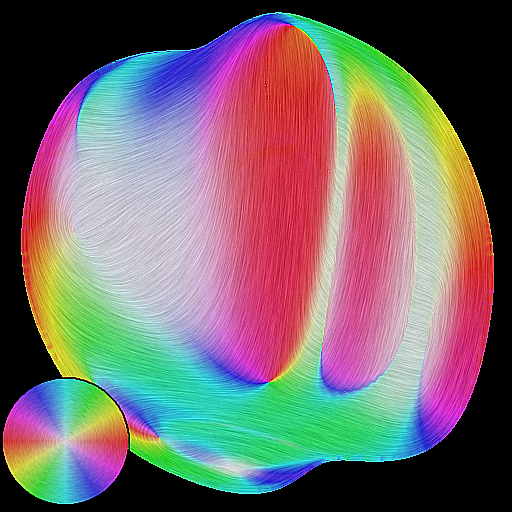
Before being able to simulate or to represent the different observed phenomena, we need to define and describe them. To understand the difference between an observed phenomenon and the classical light, shape, and matter decomposition, we can take the example of a highlight. Its observed shape (by a human user or a sensor) is the resulting process of the interaction of these three components, and can be simulated this way. However, this does not provide any intuitive understanding of their relative influence on the final shape: an artist will directly describe the resulting shape, and not each of the three properties. We thus want to decompose the observed signal into models for each scale that can be easily understandable, representable, and manipulable. For this purpose, we will rely on the analysis of the resulting interaction of light, shape, and matter as observed by a human or a physical sensor. We first consider this analysis from an optical point of view, trying to identify the different phenomena and their scale according to their mathematical properties (e.g., differential [85] and frequency analysis [48]). Such an approach has leaded us to exhibit the influence of surfaces flows (depth and normal gradients) into lighting pattern deformation (see Figure 4). For a human observer, this correspond to one recent trend in computer graphics that takes into account the human visual systems [49] both to evaluate the results and to guide the simulations.