MEMPHIS - 2016 - Annual activity report

MEMPHIS

MEMPHIS - 2016

Project-Team Memphis

Members

Overall Objectives

Multi-physics numerical modeling

Research Program

Application Domains

Highlights of the Year

New Software and Platforms

New Results

Bilateral Contracts and Grants with Industry

Bilateral Contracts with Industry

Partnerships and Cooperations

Dissemination

Bibliography

Previous |

Home | Next next

Section: New Results

Hierarchical grids: applications with quadtrees/octrees

A first application with a specific method is the resolution of the incompressible Navier-Stokes equations. A Navier-Stokes solver dealing with quadtrees has been implemented in parallel this year. The overall aim will be to model in 3D the flow over a wind turbine using an Octree grid. On the figure 18 can be seen an example of QuadTree mesh. A Finite Volume Semi-Lagrangian scheme is used.

Figure 18.



(a) Example of QuadTree mesh for circular cylinder	(b) Norms as a function of number of points on grid

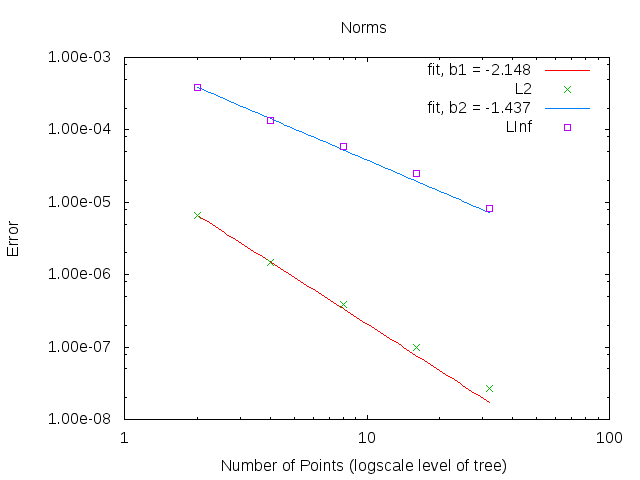
First, the order of convergence of the Laplacian Solver discretization on QuadTrees has been computed and compared with those obtained with other schemes as explained previously. The method for solving the Laplacian Solver is named Diamond method and consists in using a dual mesh and considering that the Gradients are constants inside. The order of convergence of 2 has been obtained. The order of convergence of the overall Navier-Stokes resolution on QuadTree meshes has been computed and the order of 2 is get as can be seen on figures 18. For the $L_{\infty}$ norm, the order of 2 can't be reach caused by the loss of accuracy when a gap in refinement level occurs.

For now the grid is fixed, so the next step will be to refine and coarsen the grid following the position of the obstacle and the "interesting" areas. The work will then go on with the implementation of this Navier-Stokes solver with adaptive QuadTree meshes in 3D.

A second application is phase changing material. We consider problems governed by linear elliptic equations with discontinuity interfaces across the domain. The equation coefficients, the solution and its normal derivative can undergo a jump across these internal boundaries. We present a compact second-order finite-difference scheme on a tree-based adaptive grid that can be efficiently solved in parallel. The main idea is to optimize the truncation error of the discretization as a function of the local grid configuration.

The variable coefficient heat diffusion problem we consider is modeled by:

- div (κ (\vec{x}) \nabla u (\vec{x})) = g (\vec{x}), in D,

(2)

R {(κ \partial_{\vec{n}} u (\vec{x}))}_{S} = [u], on γ

(3)

[κ (\vec{x}) \partial_{\vec{n}} u (\vec{x})] = 0, on γ

(4)

Where $\vec{x} = (x, y, z)$ are the spatial coordinates and $κ (\vec{x})$ is piecewise continuous on each subdomain but it may be discontinuous across $γ$ (the boundary of the D subdomain that contains the discontinuities through). A cell-centered investigation often leads to a symmetric linear system, since the relation between two neighbors is reflective. Considering the configuration in Fig. 19 it is natural to define the discretization at $c_{4}$ in terms of the others.

Figure 19. A test configuration centerd in

c_{4}

Let $h$ be the side length of the cell $c_{4}$ . To obtain the existence of a linear consistent scheme we must be able to find the coefficients $a_{i}$ such that:

u_{x x} + u_{y y} = a_{1} u_{1} + a_{2} u_{2} + a_{3} u_{3} + a_{4} u_{4} + a_{5} u_{5} + a_{6} u_{6} + a_{7} u_{7} + O (h)

A complete Taylor's analysis on all the involved neighbors, applying them relative linear combinations of the expansions, implies that the coefficients $a_{i}$ must satisfy the following linear system:

(\begin{matrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & - h & 0 & - h & \frac{3 h}{2} & - \frac{h}{2} & \frac{3 h}{2} \\ 0 & h & h & 0 & \frac{h}{2} & - \frac{3 h}{2} & - \frac{3 h}{2} \\ 0 & \frac{h^{2}}{2} & 0 & \frac{h^{2}}{2} & \frac{9 h^{2}}{8} & \frac{h^{2}}{8} & \frac{9 h^{2}}{8} \\ 0 & - h^{2} & 0 & 0 & \frac{3 h^{2}}{4} & \frac{3 h^{2}}{4} & - \frac{9 h^{2}}{4} \\ 0 & \frac{h^{2}}{2} & \frac{h^{2}}{2} & 0 & \frac{h^{2}}{8} & \frac{9 h^{2}}{8} & \frac{9 h^{2}}{8} \end{matrix}) (\begin{matrix} a_{4} \\ a_{1} \\ a_{2} \\ a_{3} \\ a_{5} \\ a_{6} \\ a_{7} \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \end{matrix})

In the example above there are seven concerned points, so, we can determine infinite solutions of the complete system but we search a unique one. Let $M$ be the constraints matrix, $\vec{a}$ the weights vector, $\vec{f}$ the right hand side vector for consistency and $F (\vec{a})$ a weights function. The problem to minimize has the Lagrangian form:

ℒ = F (\vec{a}) - \vec{λ} (M \vec{a} - \vec{f})

(5)

We write the minimization problem (5) in matrix form like:

A x = b \Leftrightarrow \{\begin{matrix} \frac{\partial F (\vec{a})}{\partial \vec{a}} - M^{T} \vec{λ} & = 0 \\ M \vec{a} & = \vec{f} \end{matrix}

This choice allows us to implement a scheme always consistent case by case.

Following a consistence proof several tests have been produced to strenghten our method like penalization and different kinds of model until a modeling of the problem (7.7) step by step. We built a new cell centered finite difference method able to:

be consistent and locally convergent to second order on balanced grids;
simplify and promote an AMR approach along discontinuity;
solve the coupled problems (2)-(3) and (2)-(4);
a first consistent result on the complete model (2)-(3)-(4).

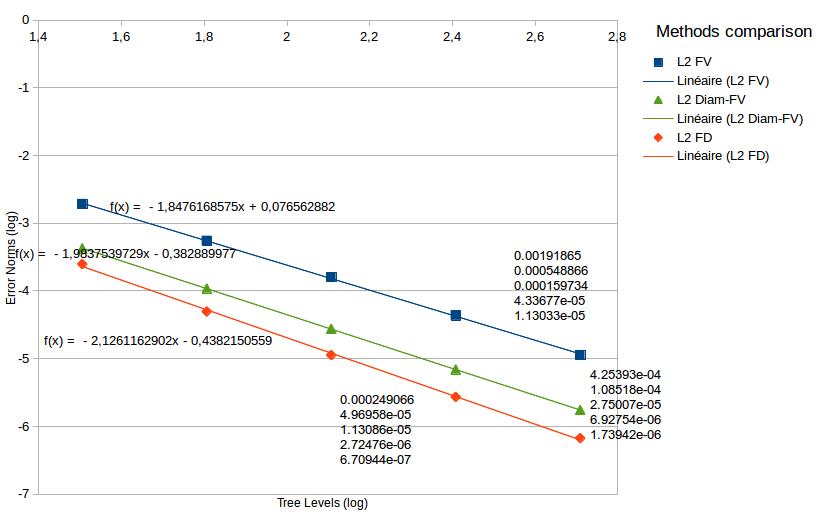
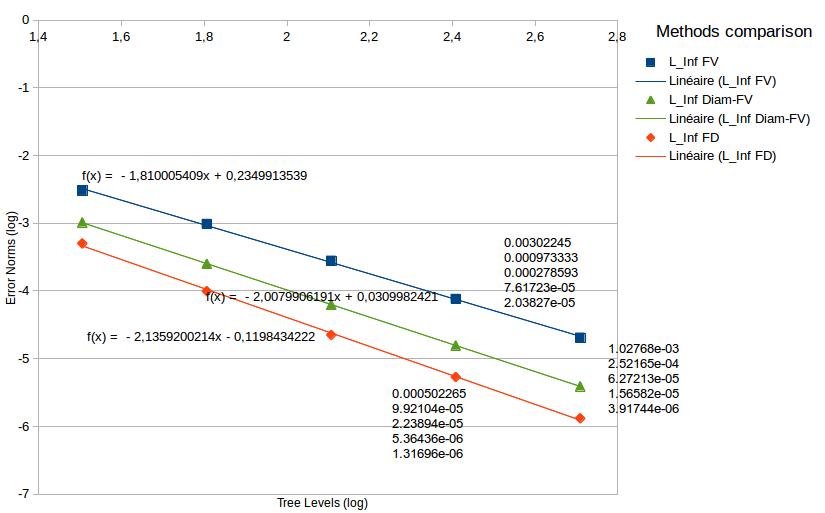
The finite different method presented here has been compared with two other methods finite volume scheme (Fig. 20). The first one has been implemented by Marco Cisternino and the diamonds one by Claire Taymans (see previous sections). All the three methods stick on the same grid and they use PABLO's data structure with its parallel balance.

Figure 20. Comparison between several numerical approaches.



(a) $L_{2}$ norm comparison	(b) $L_{\infty}$ norm comparison

Previous |

Home | Next next