Section: Application Domains
Elastodynamic wave propagation
Elastic wave propagation in interaction with solids are encountered in a lot of scientific and engineering contexts. One typical example is geoseismic wave propagation, in particular in the context of earthquake dynamics or resource prospection.
Earthquake dynamics
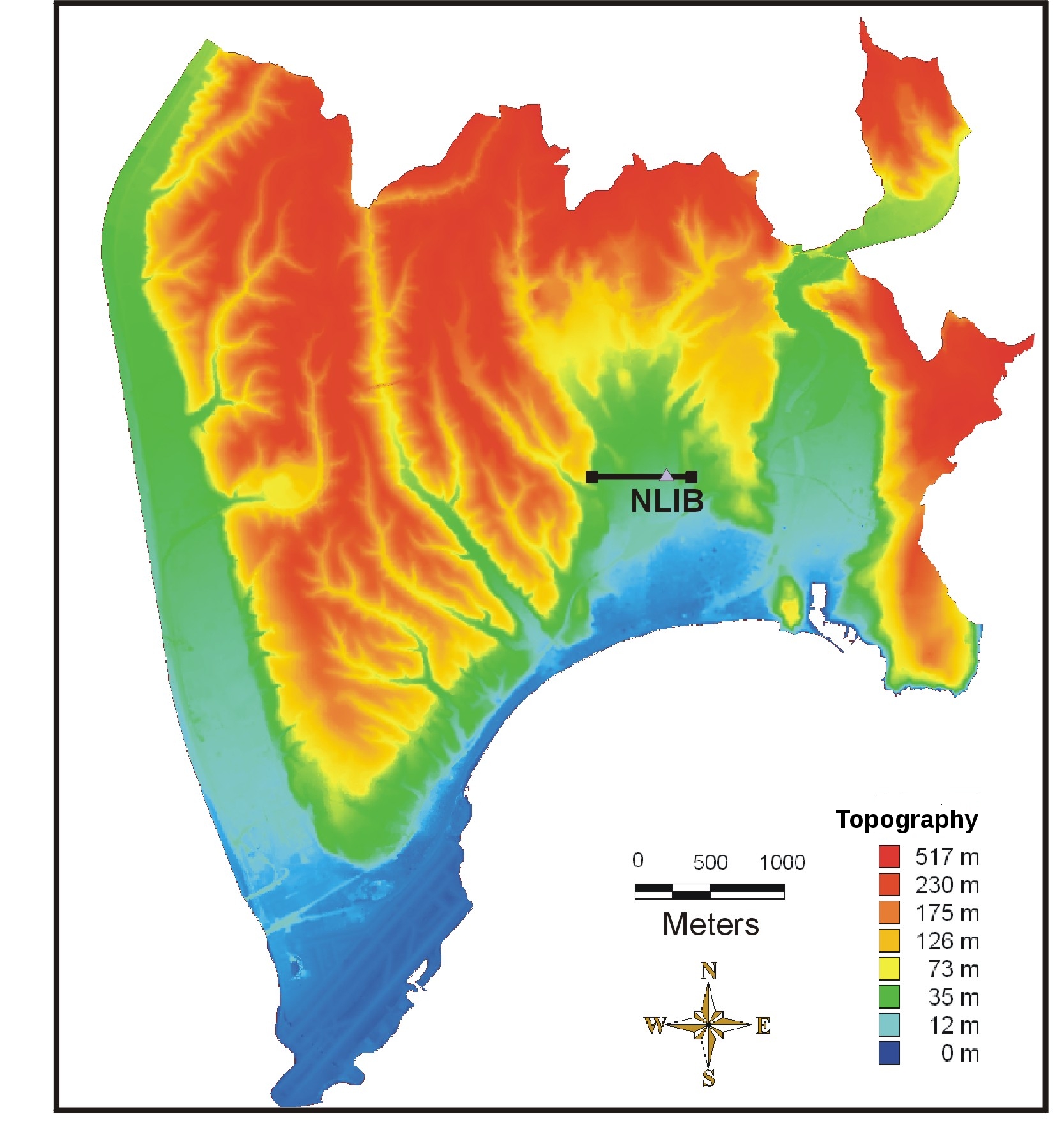
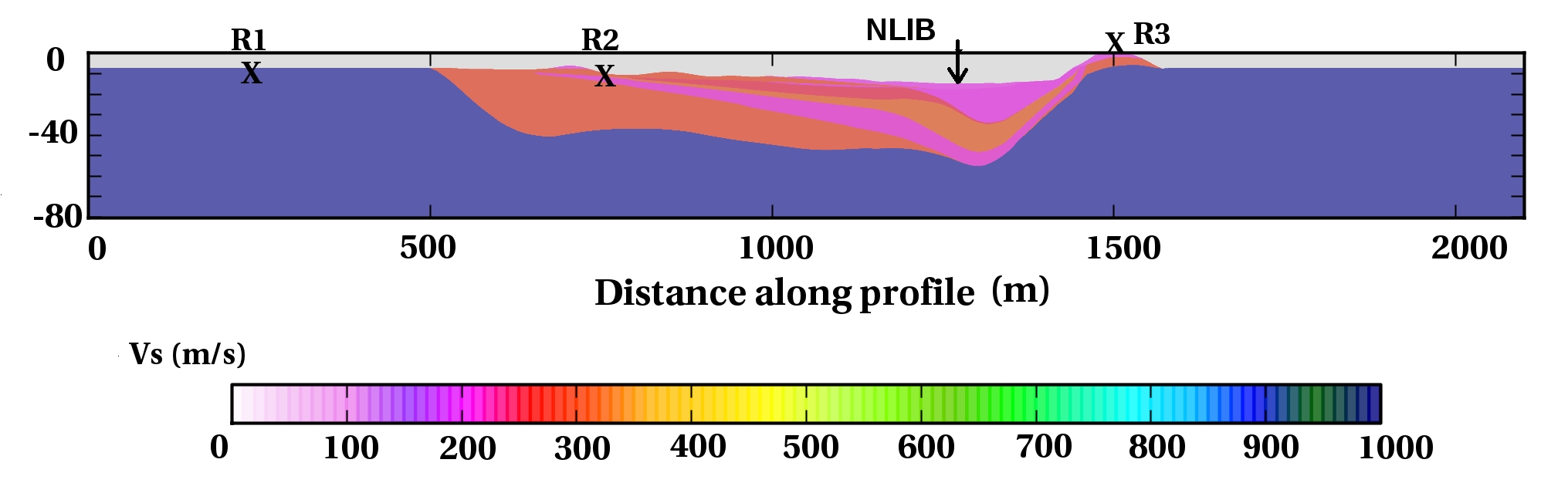
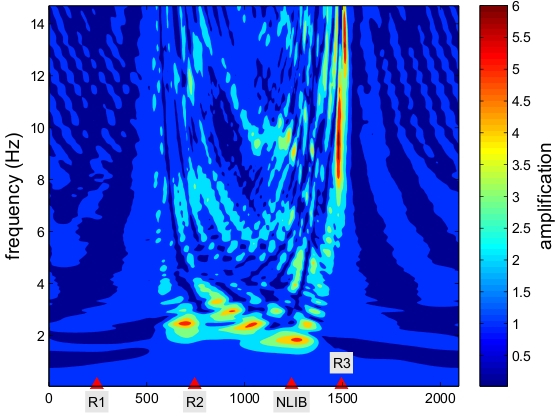
To understand the basic science of earthquakes and to help engineers better prepare for such an event, scientists want to identify which regions are likely to experience the most intense shaking, particularly in populated sediment-filled basins. This understanding can be used to improve buildings in high hazard areas and to help engineers design safer structures, potentially saving lives and property. In the absence of deterministic earthquake prediction, forecasting of earthquake ground motion based on simulation of scenarios is one of the most promising tools to mitigate earthquake related hazard. This requires intense modeling that meets the spatial and temporal resolution scales of the continuously increasing density and resolution of the seismic instrumentation, which record dynamic shaking at the surface, as well as of the basin models. Another important issue is to improve the physical understanding of the earthquake rupture processes and seismic wave propagation. Large-scale simulations of earthquake rupture dynamics and wave propagation are currently the only means to investigate these multiscale physics together with data assimilation and inversion. High resolution models are also required to develop and assess fast operational analysis tools for real time seismology and early warning systems.
Numerical methods for the propagation of seismic waves have been studied for many years. Most of existing numerical software rely on finite difference type methods. Among the most popular schemes, one can cite the staggered grid finite difference scheme proposed by Virieux [53] and based on the first order velocity-stress hyperbolic system of elastic waves equations, which is an extension of the scheme derived by Yee [54] for the solution of the Maxwell equations. Many improvements of this method have been proposed, in particular, higher order schemes in space or rotated staggered-grids allowing strong fluctuations of the elastic parameters. Despite these improvements, the use of cartesian grids is a limitation for such numerical methods especially when it is necessary to incorporate surface topography or curved interface. Moreover, in presence of a non planar topography, the free surface condition needs very fine grids (about 60 points by minimal Rayleigh wavelength) to be approximated. In this context, our objective is to develop high order unstructured mesh based methods for the numerical solution of the system of elastodynamic equations for elastic media in a first step, and then to extend these methods to a more accurate treatment of the heterogeneities of the medium or to more complex propagation materials such as viscoelastic media which take into account the intrinsic attenuation. Initially, the team has considered in detail the necessary methodological developments for the large-scale simulation of earthquake dynamics [1]. More recently, the team has initiated a close collaboration with CETE Méditerranée http://www.cete-mediterranee.fr/gb which is a regional technical and engineering centre whose activities are concerned with seismic hazard assessment studies, and IFSTTAR http://www.ifsttar.fr/en/welcome which is the French institute of science and technology for transport, development and networks, conducting research studies on control over aging, risks and nuisances.
|
Seismic exploration
This application topic is considered in close collaboration with the MAGIQUE-3D project-team at Inria Bordeaux - Sud-Ouest which is coordinating the Depth Imaging Partnership (DIP) http://dip.inria.fr between Inria and TOTAL. The research program of DIP includes different aspects of the modeling and numerical simulation of sesimic wave propagation that must be considered to construct an efficient software suites for producing accurate images of the subsurface. Our common objective with the MAGIQUE-3D project-team is to design high order unstructured mesh based methods for the numerical solution of the system of elastodynamic equations in the time-domain and in the frequency-domain, that will be used as forward modelers in appropriate inversion procedures.