Section: New Results
Stable and accurate schemes for Langevin dynamics with general kinetic energies
Participants : Zofia Trstanova, Gabriel Stoltz.
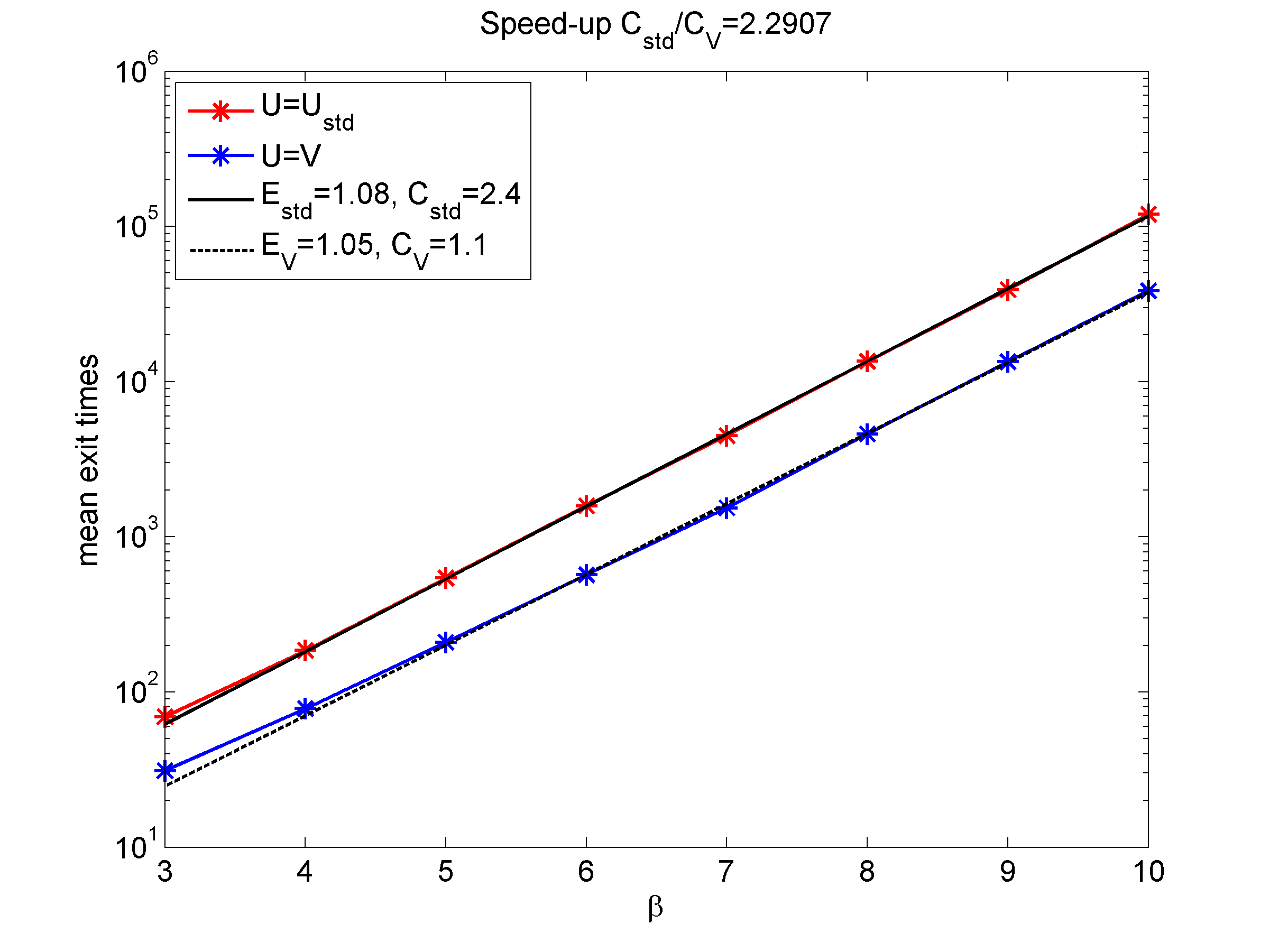
We studied integration schemes for Langevin dynamics with a kinetic energy different from the standard, quadratic one in order to accelerate the sampling of the Boltzmann–Gibbs distribution. We considered two cases: kinetic energies which are local perturbations of the standard kinetic energy around the origin, where they vanish (this corresponds to the so-called adaptively restrained Langevin dynamics); and more general non-globally Lipschitz energies. We developed numerical schemes which are stable and of weak order two, by considering splitting strategies where the discretizations of the fluctuation/dissipation are corrected by a Metropolis procedure. We used the newly developed schemes for two applications: optimizing the shape of the kinetic energy for the adaptively restrained Langevin dynamics, and reducing the metastability of some toy models with non-globally Lipschitz kinetic energies.
|