Section: New Results
Visualization and Geometric Design
Activelec: an Interaction-Based Visualization System to Analyze Household Electricity Consumption
Participants : Jérémy Wambecke, Georges-Pierre Bonneau, Romain Vergne, Renaud Blanch.
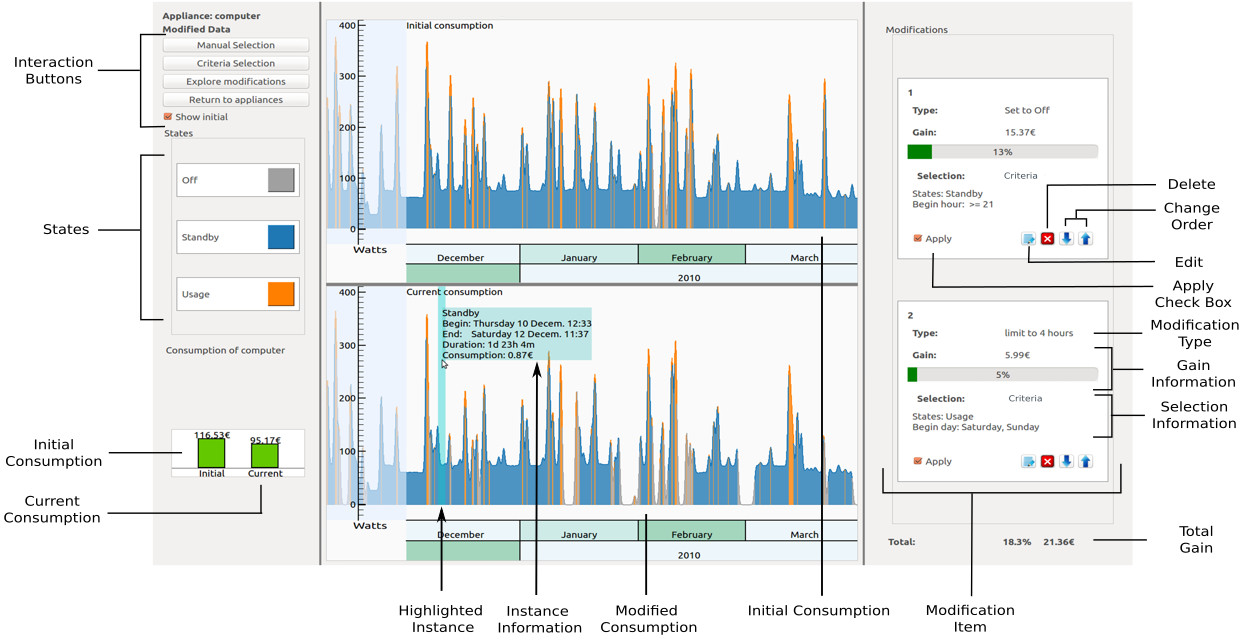
Everyone can now record and explore the evolution over time of his/her personal household electricity consumption. However understanding what links this data to our behavior remains a challenge. In this work, we present a visualization tool based on the direct manipulation, by the users, of their behavior (see Figure 13). Users can select and modify their actions over time, evaluating the results on the data with the visualization. We also conduct a user study, showing that our method allows users to understand the links between actions and data, and to use this knowledge in order to test and evaluate changesin their behavior. This work has been published in Visualization In Practice (VIP) [11].
Computing Contour Trees for 2D Piecewise Polynomial Functions
Participants : Georges-Pierre Bonneau, Stefanie Hahmann, Girijanandan Nucha, Vijay Natarajan.
|
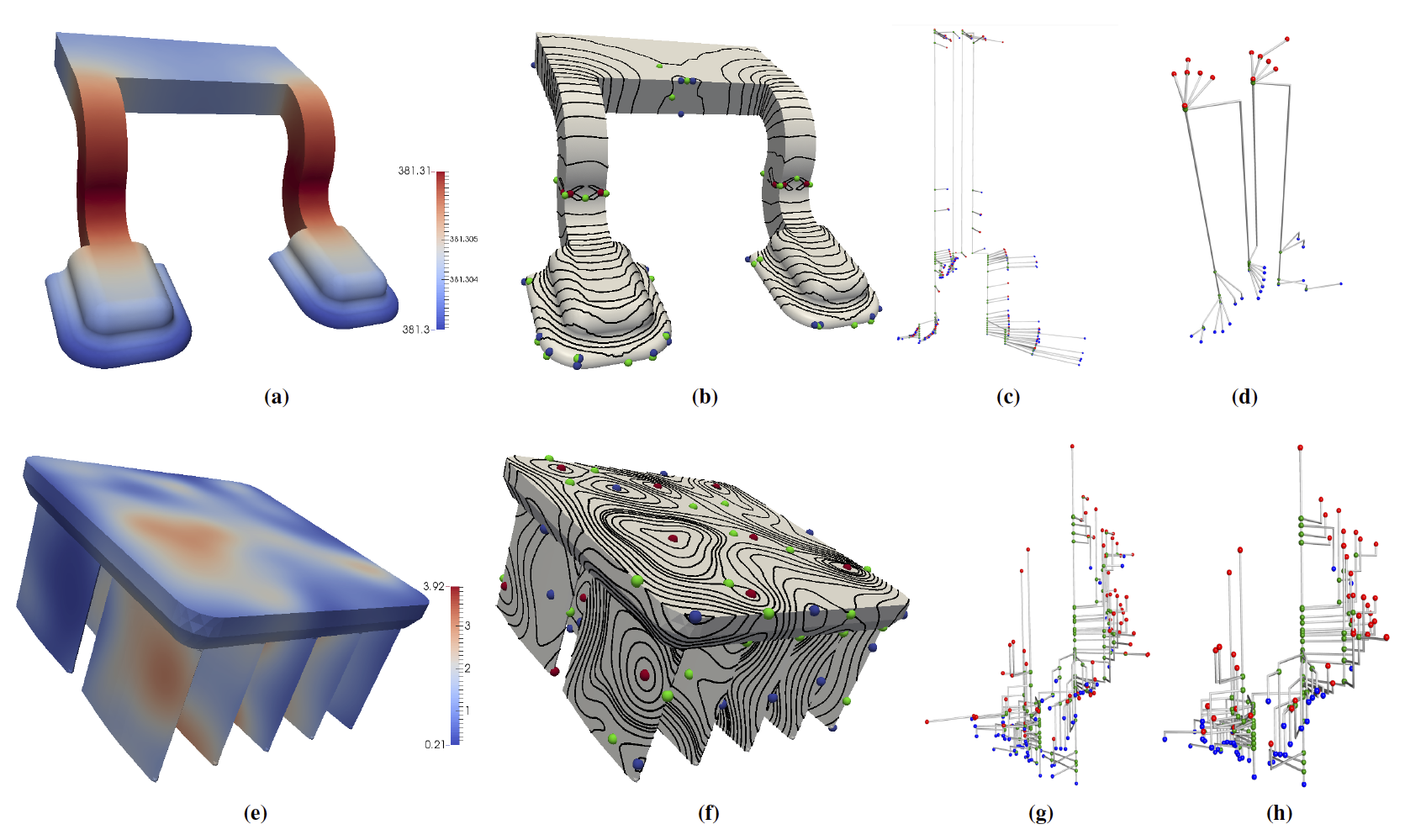
This work is a result from a collaboration with Vijay Natarajan from the Indian Institute of SCience (IISc), Bangalore, and team-project IMAGINE (Stefanie Hahmann). Contour trees are extensively used in scalar field analysis. The contour tree is a data structure that tracks the evolution of level set topology in a scalar field. Scalar fields are typically available as samples at vertices of a mesh and are linearly interpolated within each cell of the mesh. A more suitable way of representing scalar fields, especially when a smoother function needs to be modeled, is via higher order interpolants. We propose an algorithm to compute the contour tree for such functions. The algorithm computes a local structure by connecting critical points using a numerically stable monotone path tracing procedure. Such structures are computed for each cell and are stitched together to obtain the contour tree of the function. The algorithm is scalable to higher degree interpolants whereas previous methods were restricted to quadratic or linear interpolants. The algorithm is intrinsically parallelizable and has potential applications to isosurface extraction. Figure 14 shows examples of contour trees for quadratic and cubic scalar functions defined on 3D meshes. The results have been published in Computer Graphics Forum [5].
Shape from sensors: Curve networks on surfaces from 3D orientations
Participants : Tibor Stanko, Stefanie Hahmann, Georges-Pierre Bonneau, Nathalie Saguin-Sprynski.
|
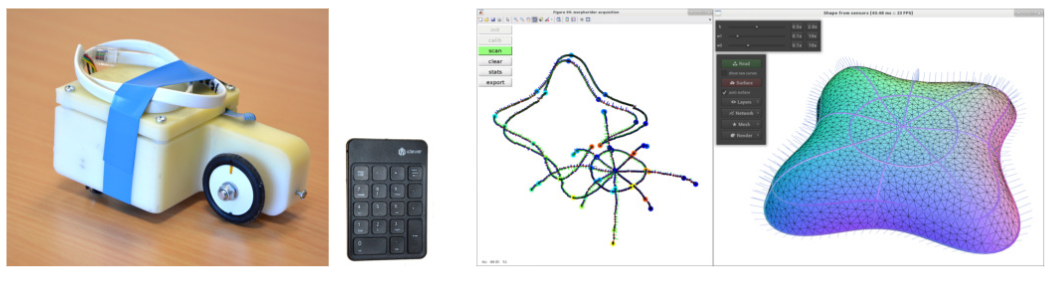
This is a joint work with team-project IMAGINE (Tibor Stanko and Stefanie Hahmann) at Inria-Grenoble and CEA-Leti (Nathalie Saguin-Sprynski). This work introduces a novel framework for acquisition and reconstruction of 3D curves using orientations provided by inertial sensors. While the idea of sensor shape reconstruction is not new, we present the first method for creating well-connected networks with cell complex topology using only orientation and distance measurements and a set of user- defined constraints. By working directly with orientations, our method robustly resolves problems arising from data inconsistency and sensor noise. Although originally designed for reconstruction of physical shapes, the framework can be used for “sketching” new shapes directly in 3D space. We test the performance of the method using two types of acquisition devices: a standard smartphone, and a custom-made device. The results have been published in C&G [6]. This paper has been awarded "Best Paper" at the conference Shape Modeling International 2017.
Morphorider: Acquisition and Reconstruction of 3D Curves with Mobile Sensors
Participants : Tibor Stanko, Stefanie Hahmann, Georges-Pierre Bonneau, Nathalie Saguin-Sprynski.
|
This is a joint work with team-project IMAGINE (Tibor Stanko and Stefanie Hahmann) at Inria-Grenoble and CEA-Leti (Nathalie Saguin-Sprynski). In this work we introduce a new mobile device called the Morphorider, which is equipped with a 3A3M-sensor node and an odometer for distance tracking. Using this single inertial measurement unit (IMU), we propose a method to scan physical objects and to reconstruct digital 3D models. By moving the IMU along the surface, a network of local orientation data is acquired together with traveled distances and network topology. We then reconstruct a consistent network of curves and fit these curves by a globally smooth surface. This work has been published in IEEE Sensors [10].