Section: New Results
Towards a continuous relaxation of the constrained problem
Participants : Gilles Aubert, Arne Henrik Bechensteen, Laure Blanc-Féraud.
We focus on the problem of minimizing the least-squares loss function under the constraint that the reconstructed signal is at maximum k-sparse. This is called the - constrained problem. The minimization problem is of interest in signal processing, with application to compressed sensing, source separation and super-resolution imaging.
This problem has previously been relaxed, among other methods, by using the convex norm instead of the norm, but depending on the specific problem the global minimizer may not be the same.
The goal of our work is to propose a continuous exact relaxation of the - constrained problem. The initial problem is non-continuous and is therefore from an algorithmic point of view difficult to minimize. A continuous exact relaxation has the same global minimizers as the initial problem, and a local minimizer of the relaxation is a local minimizer of the initial problem, with possible less local minimizers than the initial problem. Solving the initial - constrained problem is equivalent, in the sense of the global minimizers, to solving the continuous relaxed form. Furthermore, a continuous exact relaxation provides better properties for the objective function in terms of minimization, because of the continuity and the number of local minimizers.
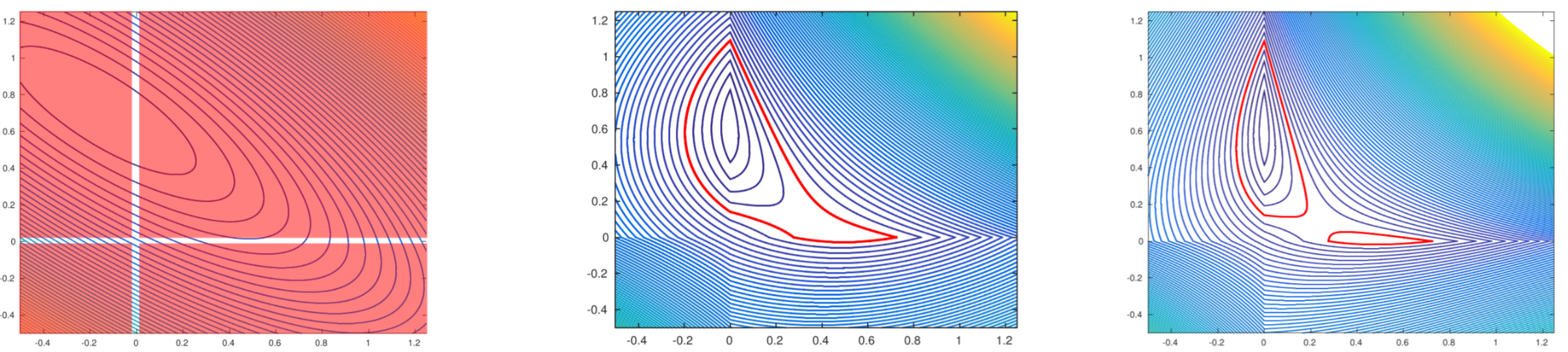
Based on the recent works of Marcus Carlson [17] we propose a continuous exact relaxation of the - constrained problem , with an algorithm to minimize the function.
In order to increase the quality of the optimization, we have to chose “the best” exact relaxation. Inspired by the work by Emmanuel Soubies [23] we have computed the convex hull of the initial problem for a special case. The penalty term obtain, may be a continuous relaxation with respect to the initial problem, with fewer local minimizers than the initial problem and the relaxation (see figure 1). This has to be proven.
|
The work will be presented at Mathematical Image Analysis 2018 conference in Berlin on the form of a poster.