Section: New Results
3D object and scene modeling, analysis, and retrieval
Congruences and Concurrent Lines in Multi-View Geometry
Participants : Jean Ponce, Bernd Sturmfels, Matthew Trager.
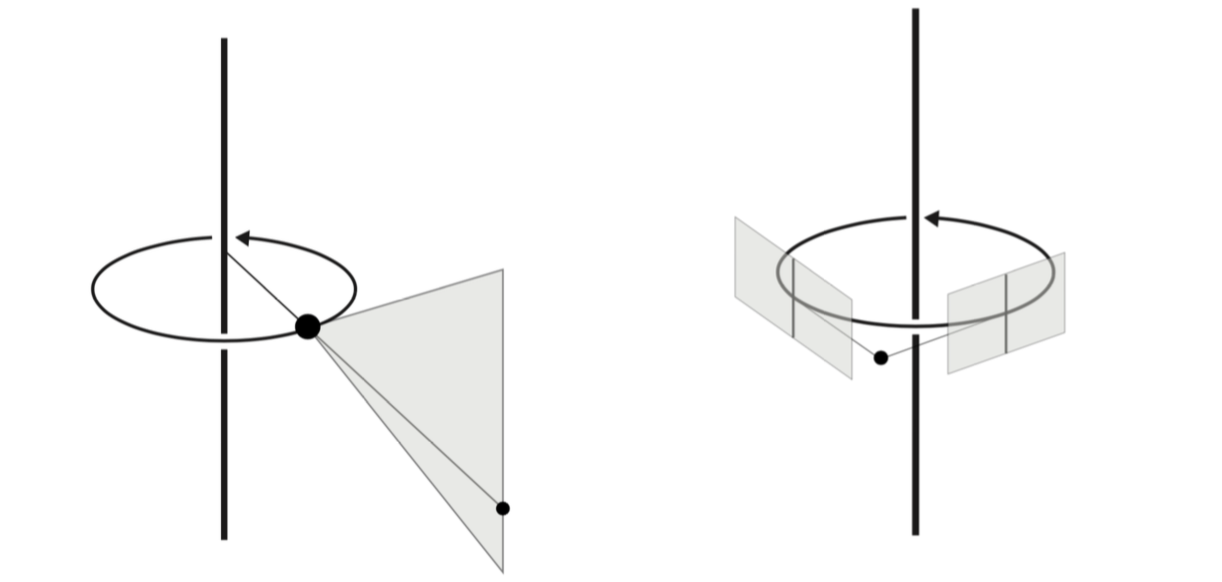
We present a new framework for multi-view geometry in computer vision. A camera is a mapping between and a line congruence. This model, which ignores image planes and measurements, is a natural abstraction of traditional pinhole cameras. It includes two-slit cameras, pushbroom cameras, catadioptric cameras, and many more (Figure 1). We study the concurrent lines variety, which consists of -tuples of lines in that intersect at a point. Combining its equations with those of various congruences, we derive constraints for corresponding images in multiple views. We also study photographic cameras which use image measurements and are modeled as rational maps from to or . This work has been published in [7].
|
General models for rational cameras and the case of two-slit projections
Participants : Matthew Trager, Bernd Sturmfels, John Canny, Martial Hebert, Jean Ponce.
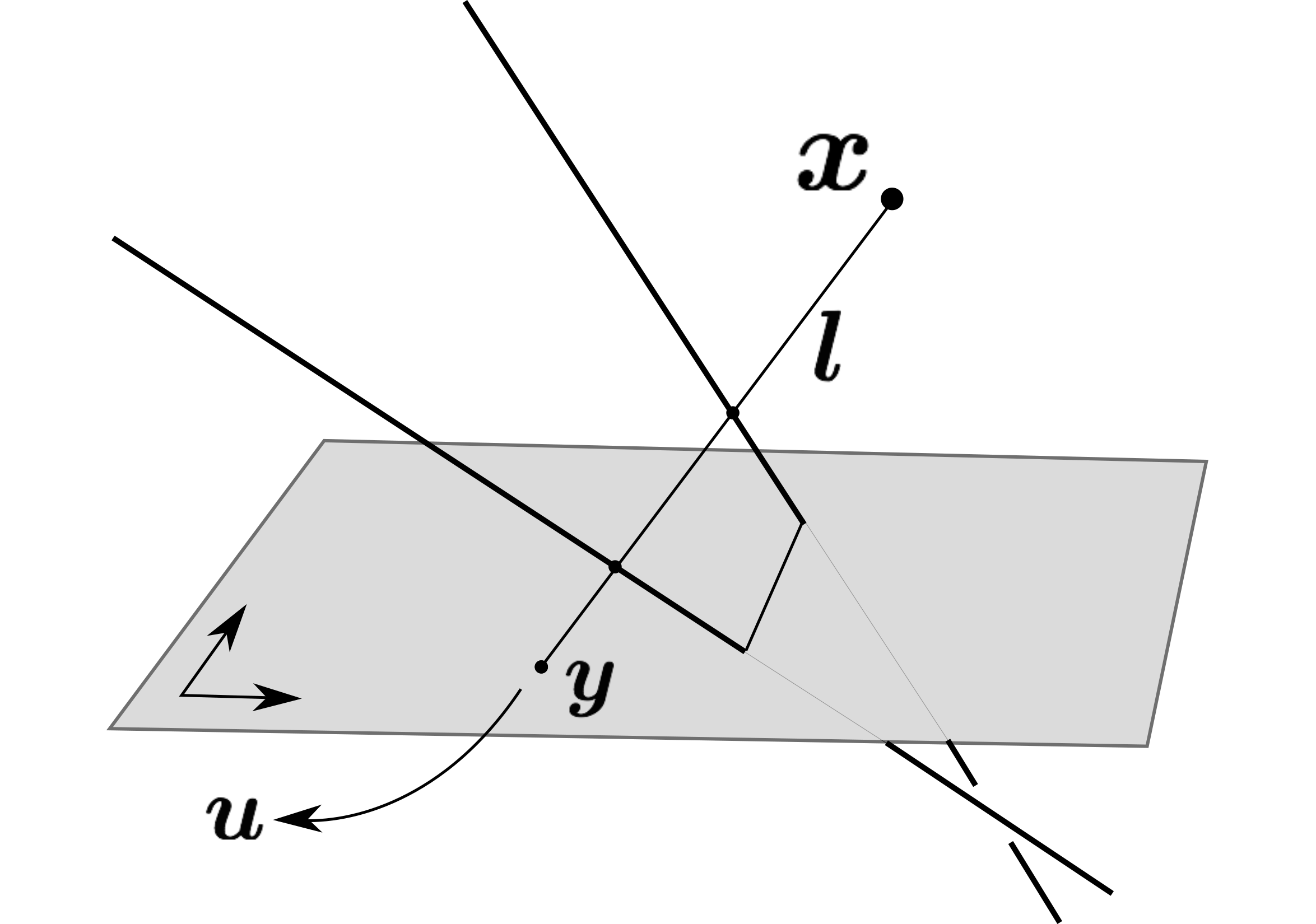
The rational camera model provides a general methodology for studying abstract nonlinear imaging systems and their multi-view geometry. This paper builds on this framework to study "physical realizations" of rational cameras. More precisely, we give an explicit account of the mapping between between physical visual rays and image points, which allows us to give simple analytical expressions for direct and inverse projections (Figure 2). We also consider "primitive" camera models, that are orbits under the action of various projective transformations, and lead to a general notion of intrinsic parameters. The methodology is general, but it is illustrated concretely by an in-depth study of two-slit cameras, that we model using pairs of linear projections. This simple analytical form allows us to describe models for the corresponding primitive cameras, to introduce intrinsic parameters with a clear geometric meaning, and to define an epipolar tensor characterizing two-view correspondences. In turn, this leads to new algorithms for structure from motion and self-calibration. This work has been published in [22].
|
Changing Views on Curves and Surfaces
Participants : Kathlén Kohn, Bernd Sturmfels, Matthew Trager.
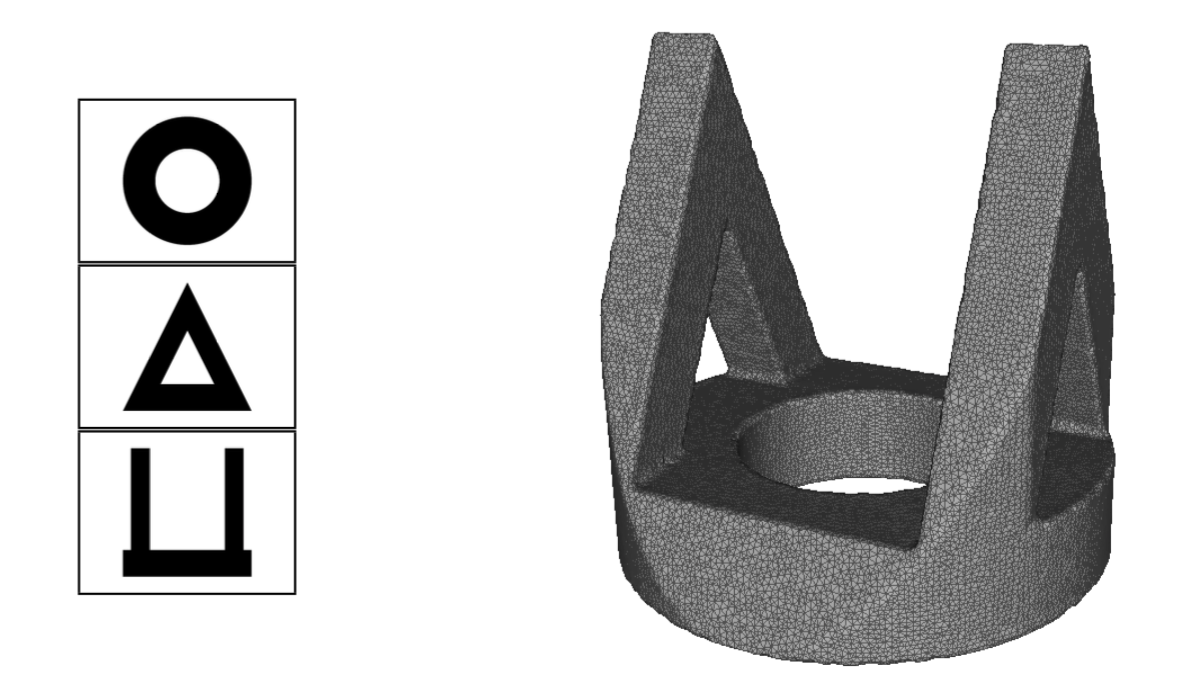
In this paper, visual events in computer vision are studied from the perspective of algebraic geometry. Given a sufficiently general curve or surface in 3-space, we consider the image or contour curve that arises by projecting from a viewpoint. Qualitative changes in that curve occur when the viewpoint crosses the visual event surface (Figure 3). We examine the components of this ruled surface, and observe that these coincide with the iterated singular loci of the coisotropic hypersurfaces associated with the original curve or surface. We derive formulas, due to Salmon and Petitjean, for the degrees of these surfaces, and show how to compute exact representations for all visual event surfaces using algebraic methods. This work was published in [6].
|
On point configurations, Carlsson-Weinshall duality, and multi-view geometry
Participants : Matthew Trager, Martial Hebert, Jean Ponce.
We propose in this project projective point configurations as a natural setting for studying perspective projection in a geometric, coordinate-free manner. We show that classical results on the effect of permutations on point configurations give a purely synthetic formulation of the well known analytical Carlsson-Weinshall duality between camera pinholes and scene points. We further show that the natural parameterizations of configurations in terms of subsets of their points provides a new and simple analytical formulation of Carlsson-Weinshall duality in any scene and image coordinate systems, not just in the reduced coordinate frames used traditionally. When working in such reduced coordinate systems, we give a new and complete characterization of multi-view geometry in terms of a reduced joint image and its dual. We also introduce a new parametrization of trinocular geometry in terms of reduced trilinearities, and show that, unlike trifocal tensors, these are not subject to any nonlinear internal constraints. This leads to purely linear primal and dual structure-from-motion algorithms, that we demonstrate with a preliminary implementation on real data. This work has been submitted to CVPR'18 [27].
Are Large-Scale 3D Models Really Necessary for Accurate Visual Localization?
Participants : Torsten Sattler, Akihiko Torii, Josef Sivic, Marc Pollefeys, Hajime Taira, Masatoshi Okutomi, Tomas Pajdla.
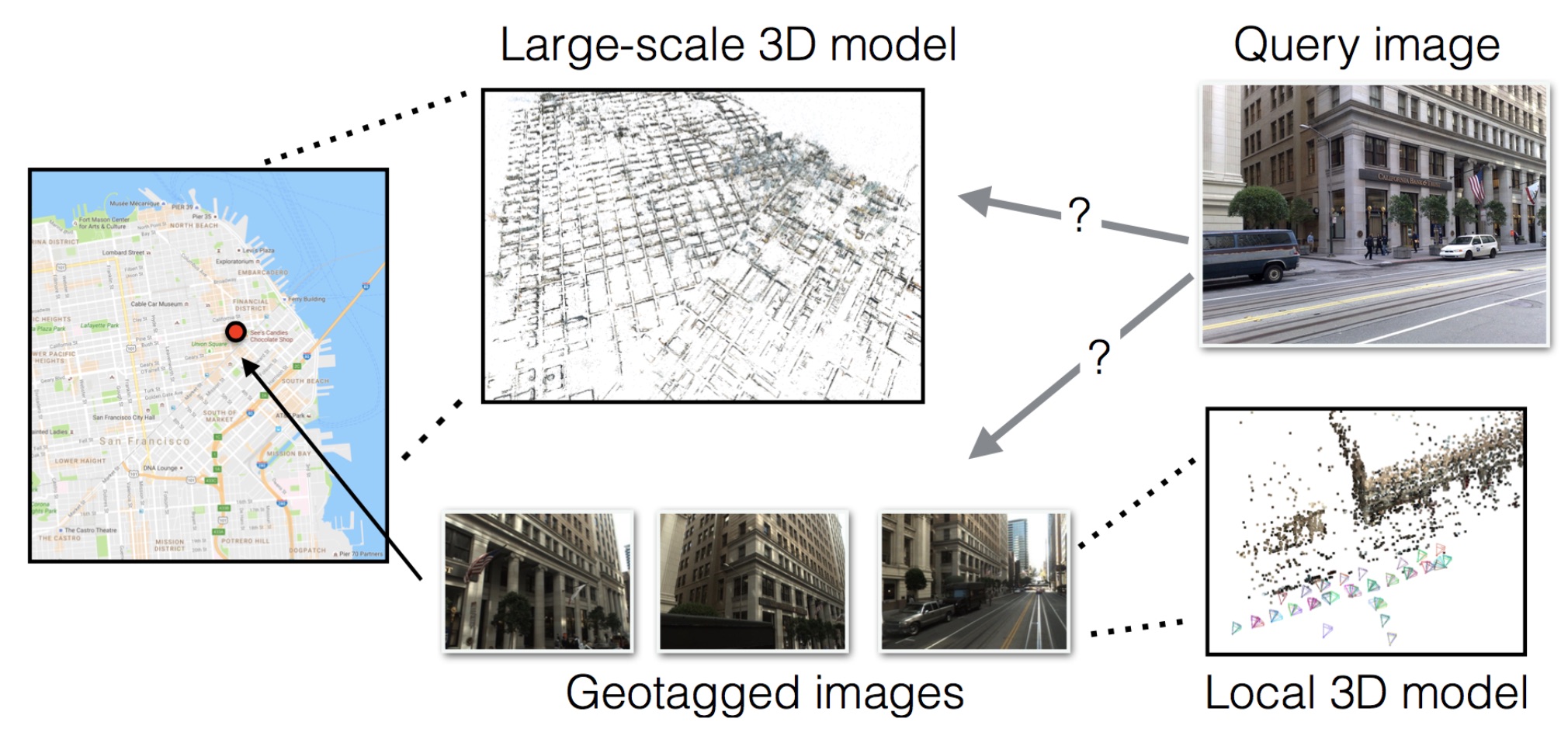
Accurate visual localization is a key technology for autonomous navigation. 3D structure-based methods employ 3D models of the scene to estimate the full 6DOF pose of a camera very accurately. However, constructing (and extending) large-scale 3D models is still a significant challenge. In contrast, 2D image retrieval-based methods only require a database of geo-tagged images, which is trivial to construct and to maintain. They are often considered inaccurate since they only approximate the positions of the cameras. Yet, the exact camera pose can theoretically be recovered when enough relevant database images are retrieved. In this paper, we demonstrate experimentally that large-scale 3D models are not strictly necessary for accurate visual localization. We create reference poses for a large and challenging urban dataset. Using these poses, we show that combining image-based methods with local reconstructions results in a pose accuracy similar to the state-of-the-art structure-based methods. Our results, published at [21] and illustrated in Figure 4, suggest that we might want to reconsider the current approach for accurate large-scale localization.
|