Section: New Results

Exact biconvex reformulation of the ${\ell }_2-{\ell }_0$ minimization problem

Participants : Gilles Aubert, Arne Henrik Bechensteen, Laure Blanc-Féraud.

We focus on the problem of minimizing the least-squares loss function under the constraint that the reconstructed signal is at maximum k-sparse. This is called the ${\ell }_2$-${\ell }_0$ constrained problem. The ${\ell }_0$ pseudo-norm counts the number of non-zero elements in a vector. The minimization problem is of interest in signal processing, with a wide range of applications such as compressed sensing, source separation, and super-resolution imaging.

Based on the results of [20], we reformulate the ${\ell }_0$ pseudo-norm exactly as a convex minimization problem by introducing an auxiliary variable. We then propose an exact biconvex reformulation of the ${\ell }_2-{\ell }_0$ constrained and penalized problems. We give correspondence results between minimizer of the initial function and the reformulated ones. The reformulation is biconvex. This property is used to derive a minimization algorithm.

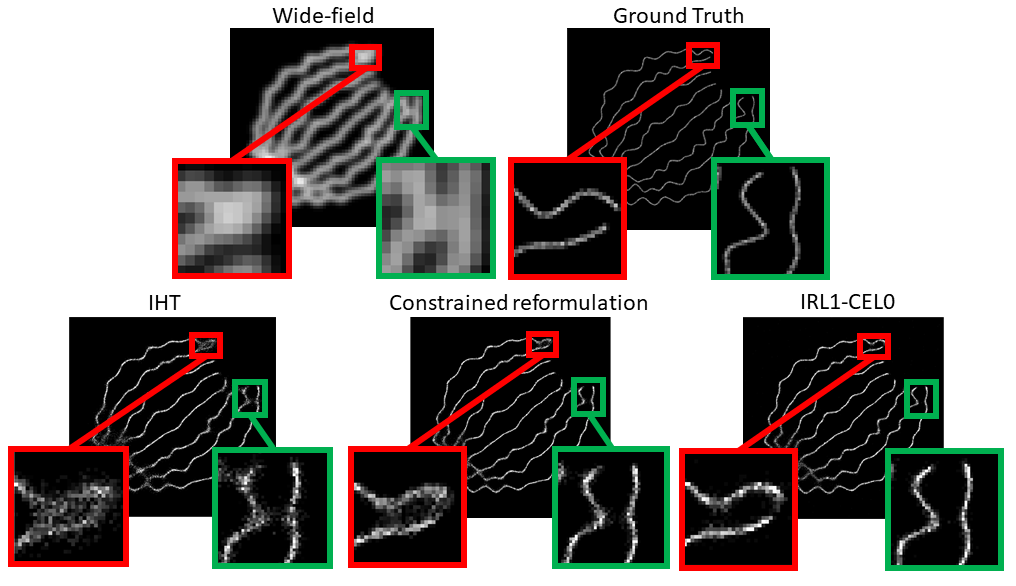
We apply the algorithm to the problem of Single-Molecule Localization Microscopy and compare the results with the well-known IHT algorithm [13]. Both visually and numerically the biconvex reformulations perform better. This work has been presented at the iTWIST 2018 workshop [5].

Furthermore, the algorithm has been compared to the IRL1-CEL0 [14] and Deep-STORM [15] (see figure 1). The IRL1-CEL0 minimizes an exact relaxation [19] of the ${\ell }_2-{\ell }_0$ penalized form and Deep-STORM is an algorithm that uses deep-learning and convolutional network to localize the molecules. This work has been accepted to the ISBI 2019 conference.

Figure 1. Reconstruction by the different algorithms. Data set from ISBI 2013 challenge [18].