Section: New Results
3D object and scene modeling, analysis, and retrieval
Indoor Visual Localization with Dense Matching and View Synthesis
Participants : Hajime Taira, Masatoshi Okutomi, Torsten Sattler, Mircea Cimpoi, Marc Pollefeys, Josef Sivic, Tomas Pajdla, Akihiko Torii.
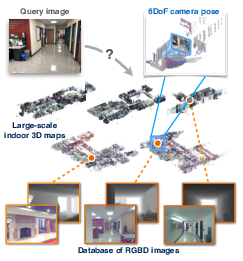
In [20], we seek to predict the 6 degree-of-freedom (6DoF) pose of a query photograph with respect to a large indoor 3D map. The contributions of this work are three-fold. First, we develop a new large-scale visual localization method targeted for indoor environments. The method proceeds along three steps: (i) efficient retrieval of candidate poses that ensures scalability to large-scale environments, (ii) pose estimation using dense matching rather than local features to deal with textureless indoor scenes, and (iii) pose verification by virtual view synthesis to cope with significant changes in viewpoint, scene layout, and occluders. Second, we collect a new dataset with reference 6DoF poses for large-scale indoor localization. Query photographs are captured by mobile phones at a different time than the reference 3D map, thus presenting a realistic indoor localization scenario. Third, we demonstrate that our method significantly outperforms current state-of-the-art indoor localization approaches on this new challenging data. Figure 1 presents some example results.
|
Benchmarking 6DOF Outdoor Visual Localization in Changing Conditions
Participants : Torsten Sattler, Will Maddern, Carl Toft, Akihiko Torii, Lars Hammarstrand, Erik Stenborg, Daniel Safari, Masatoshi Okutomi, Marc Pollefeys, Josef Sivic, Frederik Kahl, Tomas Pajdla.
Visual localization enables autonomous vehicles to navigate in their surroundings and augmented reality applications to link virtual to real worlds. Practical visual localization approaches need to be robust to a wide variety of viewing condition, including day-night changes, as well as weather and seasonal variations, while providing highly accurate 6 degree-of-freedom (6DOF) camera pose estimates. In [19], we introduce the first benchmark datasets specifically designed for analyzing the impact of such factors on visual localization. Using carefully created ground truth poses for query images taken under a wide variety of conditions, we evaluate the impact of various factors on 6DOF camera pose estimation accuracy through extensive experiments with state-of-the-art localization approaches. Based on our results, we draw conclusions about the difficulty of different conditions, showing that long-term localization is far from solved, and propose promising avenues for future work, including sequence-based localization approaches and the need for better local features. Our benchmark is available at visuallocalization.net. Figure 2 presents some example results.
|
Changing Views on Curves and Surfaces
Participants : Kathlen Kohn, Bernd Sturmfels, Matthew Trager.
Participants : Boris Bukh, Xavier Goaoc, Alfredo Hubard, Matthew Trager.
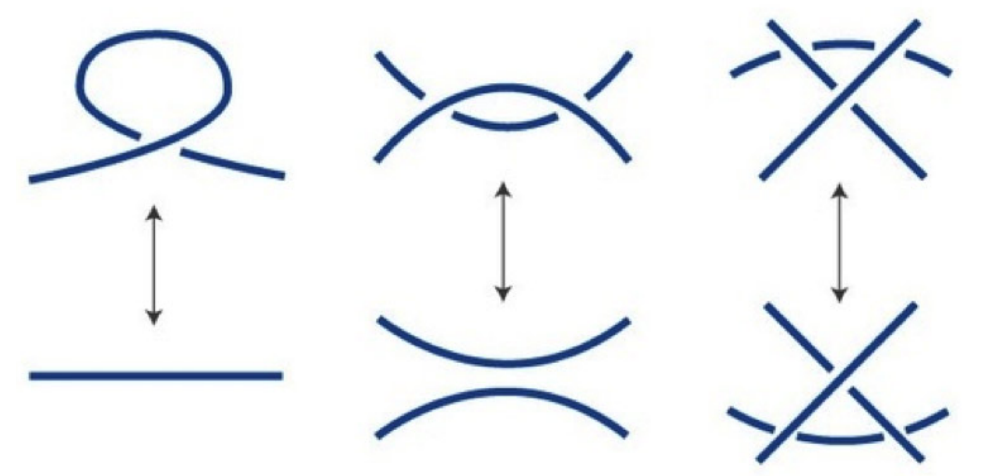
Visual events in computer vision are studied from the perspective of algebraic geometry. Given a sufficiently general curve or surface in 3-space, we consider the image or contour curve that arises by projecting from a viewpoint. Qualitative changes in that curve occur when the viewpoint crosses the visual event surface as illustrated in 3. We examine the components of this ruled surface, and observe that these coincide with the iterated singular loci of the coisotropic hypersurfaces associated with the original curve or surface. We derive formulas, due to Salmon and Petitjean, for the degrees of these surfaces, and show how to compute exact representations for all visual event surfaces using algebraic methods. This work has been published in [8].
|
subsectionConsistent Sets of Lines with no Colorful Incidence
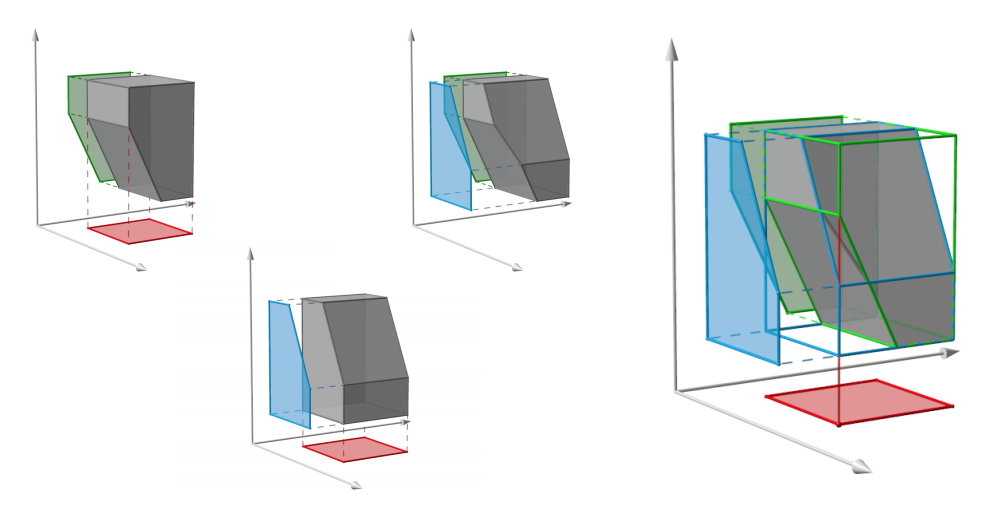
We consider incidences among colored sets of lines in and examine whether the existence of certain concurrences between lines of colors force the existence of at least one concurrence between lines of colors. This question is relevant for problems in 3D reconstruction in computer vision such as the one illustrated in Figure 4. This work has been published in [12].
|
On the Solvability of Viewing Graphs
Participants : Matthew Trager, Brian Osserman, Jean Ponce.
A set of fundamental matrices relating pairs of cameras in some configuration can be represented as edges of a ” viewing graph ". Whether or not these fundamental matrices are generically sufficient to recover the global camera configuration depends on the structure of this graph. We study characterizations of ” solvable " viewing graphs, and present several new results that can be applied to determine which pairs of views may be used to recover all camera parameters. We also discuss strategies for verifying the solvability of a graph computationally. This work has been published in [21].
In Defense of Relative Multi-View Geometry
Participants : Matthew Trager, Jean Ponce.
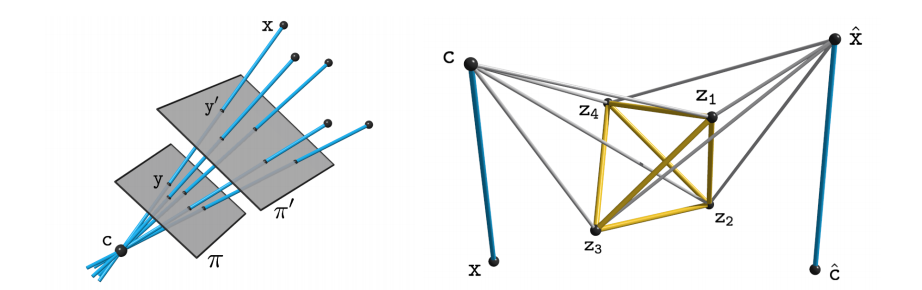
The idea of studying multi-view geometry and structure-from-motion problems relative to the scene and camera configurations, without appeal to external coordinate systems, dates back to the early days of modern geometric computer vision. Yet, it has a bad rap, the scene reconstructions obtained often being deemed as inaccurate despite careful implementations. The aim of this article is to correct this perception with a series of new results. In particular, we show that using a small subset of scene and image points to parameterize their relative configurations offers a natural coordinate-free formulation of Carlsson-Weinshall duality for arbitrary numbers of images. An example is shown in Figure 5. For three views, this approach also yields novel purely- and quasi-linear formulations of structure from motion using reduced trilinearities, without the complex polynomial constraints associated with trifocal tensors, revealing in passing the strong link between “3D” () and “2D” () models of trinocular vision. Finally, we demonstrate through preliminary experiments that the proposed relative reconstruction methods gives good results on real data. This works is available as a preprint [32].
|
Multigraded Cayley-Chow Forms
Participants : Brian Osserman, Matthew Trager.
We introduce a theory of multigraded Cayley-Chow forms associated to subvarieties of products of projective spaces. Figure 6 illustrares some examples of projective speces. Two new phenomena arise: first, the construction turns out to require certain inequalities on the dimensions of projections; and second, in positive characteristic the multigraded Cayley-Chow forms can have higher multiplicities. The theory also provides a natural framework for understanding multifocal tensors in computer vision. This works is available as a preprint [30].