Section: New Results

Electromagnetic wave propagation

POD-based reduced-order DGTD method

Participants : Stéphane Lanteri, Kun Li [UESTC, Chengdu, China] , Liang Li [UESTC, Chengdu, China] .

This study is concerned with reduced-order modeling for time-domain electromagnetics and nanophotonics. More precisely, we consider the applicability of the proper orthogonal decomposition (POD) technique for the system of 3D time-domain Maxwell equations, possibly coupled to a Drude dispersion model, which is employed to describe the interaction of light with nanometer scale metallic structures. We introduce a discontinuous Galerkin (DG) approach for the discretization of the problem in space based on an unstructured tetrahedral mesh. A reduced subspace with a significantly smaller dimension is constructed by a set of POD basis vectors extracted offline from snapshots that are obtained by the global DGTD scheme with a second order leap-frog method for time integration at a number of time levels. POD-based ROM is established by projecting (Galerkin projection) the global semi-discrete DG scheme onto the low-dimensional space. The stability of the POD-based ROM equipped with the second order leap-frog time scheme has been analysed through an energy method. Numerical experiments have allowed to verify the accuracy, and demonstrate the capabilities of the POD-based ROM. These very promising preliminary results are currently consolidated by assessing the efficiency of the proposed POD-based ROM when applied to the simulation of 3D nanophotonic problems.

Study of 3D periodic structures at oblique incidences

Participants : Claire Scheid, Nikolai Schmitt, Jonathan Viquerat.

In this work, we focus on the development of the use of periodic boundary conditions with sources at oblique incidence in a DGTD framework. Whereas in the context of the Finite Difference Time Domain (FDTD) methods, an abundant literature can be found, for DGTD, the amount of contributions reporting on such methods is remarkably low. In this work, we supplement the existing references using the field transform technique with an analysis of the continuous system using the method of characteristics and provide an energy estimate. Furthermore, we also study the numerical stability of the resulting DGTD scheme. After numerical validations, two realistic test problems have been considered in the context of nanophotonics with our DIOGENeS DGTD solver. This work has been accepted for publication in 2019.

Stability and asymptotic properties of the linearized Hydrodynamic Drude model

Participants : Serge Nicaise [Université de Valenciennes] , Claire Scheid.

We go a step further toward a better understanding of the fundamental properties of the linearized hydrodynamical model studied in the PhD of Nikolai Schmitt [16]. This model is especially relevant for small nanoplasmonic structures (below 10nm). Using a hydrodynamical description of the electron cloud, both retardation effects and non local spatial response are taken into account. This results in a coupled PDE system for which we study the linear response. In [45] (submitted, under revision), we concentrate on establishing well posedness results combined to a theoretical and numerical stability analysis. We especially prove polynomial stability and provide optimal energy decay rate. Finally, we investigate the question of numerical stability of several explicit time integration strategies combined to a Discontinuous Galerkin spatial discretization.

Toward thermoplasmonics

Participants : Yves d'Angelo, Stéphane Lanteri, Claire Scheid.

Although losses in metal is viewed as a serious drawback in many plasmonics experiments, thermoplasmonics is the field of physics that tries to take advantage of the latter. Indeed, the strong field enhancement obtained in nanometallic structures lead to a localized raise of the temperature in its vicinity leading to interesting photothermal effects. Therefore, metallic nanoparticles may be used as heat sources that can be easily integrated in various environments. This is especially appealing in the field of nanomedecine and can for example be used for diagnosis purposes or nanosurgery to cite but just a few. This year, we initiated a preliminary work towards this new field in collaboration with Y. D'Angelo (Université Côte d'Azur) and G. Baffou (Fresnel Institute, Marseille) who is an expert in this field. Due to the various scales and phenomena that come into play, the numerical modeling present great challenges. The laser illumination first excite a plasmon oscillation (reaction of the electrons of the metal) that relaxes in a thermal equilibrium and in turn excite the metal lattice (phonons). The latter is then responsible for heating the environment. A relevant modeling approach thus consists in describing the electron-phonon coupling through the evolution of their respective temperature. Maxwell's equations is then coupled to a set of coupled nonlinear hyperbolic equations describing the evolution of the temperatures of electrons, phonons and environment. The nonlinearities and the different time scales at which each thermalization occurs make the numerical approximation of these equations quite challenging.

Corner effects in nanoplasmonics

Participants : Camille Carvalho [Applied Mathematics Department, University of California Merced, USA] , Claire Scheid.

In this work, we study nanoplasmonic structures with corners (typically a diedral/triangular structure); a situation that raises a lot of issues. We focus on a lossles Drude dispersion model and propose to investigate the range of validity of the amplitude limit principle. The latter predicts the asymptotic harmonic regime of a structure that is monochromatically illuminated, which makes a frequency domain approach relevant. However, in frequency domain, several well posedness problems arise due to the presence of corners (addressed in the PhD thesis of Camille Carvalho). This should impact the validity of the limit amplitude principle and has not yet been addressed in the literature in this precise setting. Here, we combine frequency-domain and time-domain viewpoints to give a numerical answer to this question in two dimensions. We show that the limit amplitude principle does not hold for whole interval of frequencies, that are explicited using the well-posedness analysis. This work is now being finalized.

MHM methods for the time-domain Maxwell equations

Participants : Alexis Gobé, Stéphane Lanteri, Diego Paredes Concha [Instituto de Matemáticas, Universidad Católica de Valparaiso, Chile] , Claire Scheid, Frédéric Valentin [LNCC, Petropolis, Brazil] .

Although the DGTD method has already been successfully applied to complex electromagnetic wave propagation problems, its accuracy may seriously deteriorate on coarse meshes when the solution presents multiscale or high contrast features. In other physical contexts, such an issue has led to the concept of multiscale basis functions as a way to overcome such a drawback and allow numerical methods to be accurate on coarse meshes. The present work, which is conducted in the context of the HOMAR Associate Team, is concerned with the study of a particular family of multiscale methods, named Multiscale Hybrid-Mixed (MHM) methods. Initially proposed for fluid flow problems, MHM methods are a consequence of a hybridization procedure which caracterize the unknowns as a direct sum of a coarse (global) solution and the solutions to (local) problems with Neumann boundary conditions driven by the purposely introduced hybrid (dual) variable. As a result, the MHM method becomes a strategy that naturally incorporates multiple scales while providing solutions with high order accuracy for the primal and dual variables. The completely independent local problems are embedded in the upscaling procedure, and computational approximations may be naturally obtained in a parallel computing environment. In this study, a family of MHM methods is proposed for the solution of the time-domain Maxwell equations where the local problems are discretized either with a continuous FE method or a DG method (that can be viewed as a multiscale DGTD method). Preliminary results have been obtained in the two-dimensional case.

HDG methods for the time-domain Maxwell equations

Participants : Théophile Chaumont-Frelet, Stéphane Descombes, Stéphane Lanteri, Georges Nehmetallah.

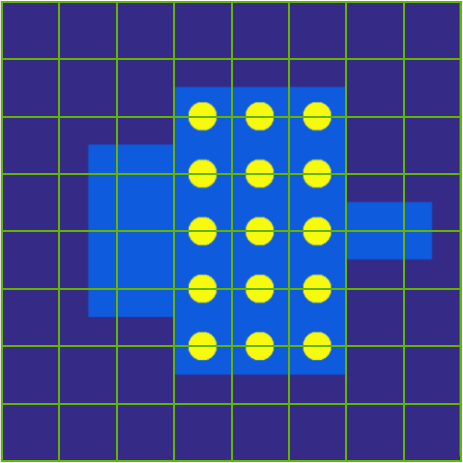
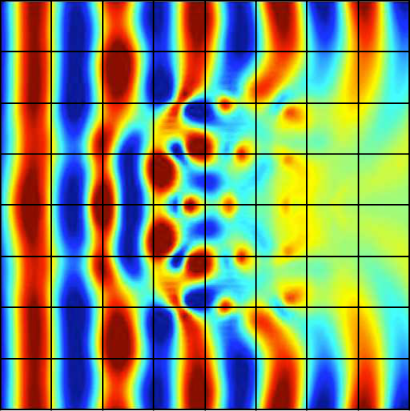
Hybridizable discontinuous Galerkin (HDG) methods have been investigated in the team since 2012. This family of method employs face-based degrees of freedom that can be viewed as a fine grain domain decomposition technique. We originally focused on frequency-domain applications, for which HDG methods enable the use of static condensation, leading to drastic reduction in computational time and memory consumption. More recently, we have investigated the use of HDG discretization to solve time-dependent problems. Specifically, in the context of the PhD thesis of Georges Nehmetallah, we focused on two particular aspects. On the one hand, HDG methods exhibit a superconvergence property that allows, by means of local postprocessing, to obtain new improved approximations of the unknowns. Our first contribution is to apply this methodology to time-dependent Maxwell's equations, where the post-processed approximation converges with order $k+1$ instead of $k$ in the $H\left(curl\right)$-norm, when using polynomial of degree $k\ge 1$. The proposed method has been implemented for dealing with general 3D problems. Fig. 5 highlights the improved accuracy of the post-processed approximation on a cavity benchmark.

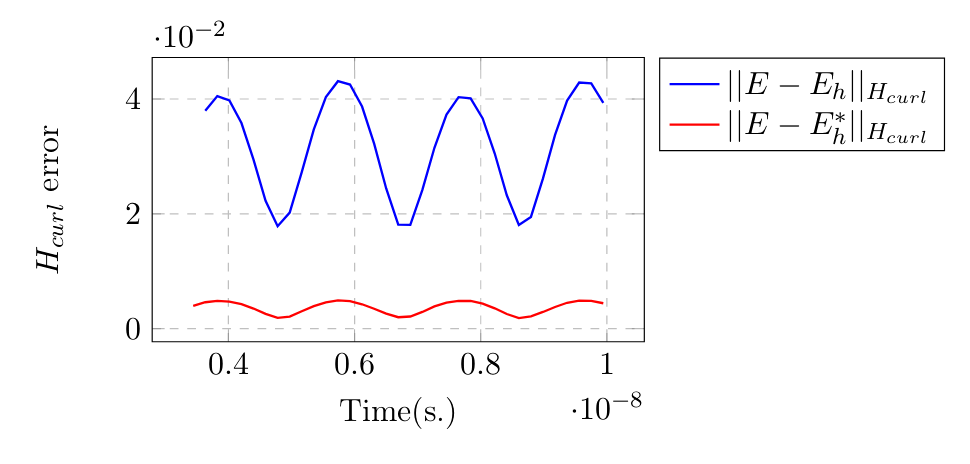
Another interesting aspect of the HDG method is that it can be conveniently employed to blend different time-integration schemes in different regions of the mesh. This is especially useful to efficiently handle locally refined space grids, that are required to take into account geometrical details. These ideas have already been explored for standard discontinuous Galerkin discretization in the context of the PhD thesis of Ludovic Moya [13], [14]. Here, we focused on HDG methods and we introduced a family of coupled implicit-explicit (IMEX) time integration methods for solving time-dependent Maxwell's equations. We established stability conditions that are independent of the size of the small elements in the mesh, and are only constrained by the coarse part. Numerical experiments on two-dimensional benchmarks illustrate the theory and the usefulness of the approach.

A posteriori error estimators

Participants : Théophile Chaumont-Frelet, Alexandre Ern [SERENA project-team] , Patrick Vega, Martin Vohralík [SERENA project-team] .

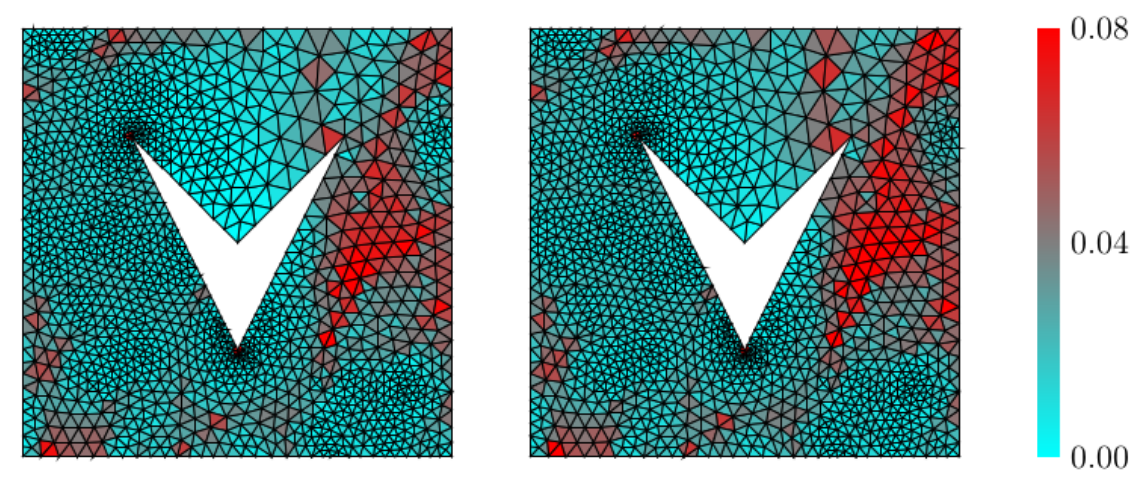
The development of a posteriori error estimators and is a new topic of interest for the team. Concerning a posteriori estimators, a collaboration with the SERENA project-team has been initiated. We mainly focus on a technique called equilibrated fluxes, which has the advantage to produce $p$-robust error estimators together with guaranteed error estimates. This means in particular that these estimators are particularly suited for high-order discretization schemes. Our first results deal with the Helmholtz equation, and have been recently submitted [39] and presented at the Enumath international conference [29]. Fig. 6 depicts the ability of the estimators to accurately describe the error distribution in a realistic application. Future works in this line will include the treatment of Maxwell's equations. The recently hired postdoctoral fellow Patrick Vega will actively participate in these developments.

$hp$-adaptivity

Participants : Théophile Chaumont-Frelet, David Pardo [Basque Center for Applied Mathematics, Bilbao, Spain] .

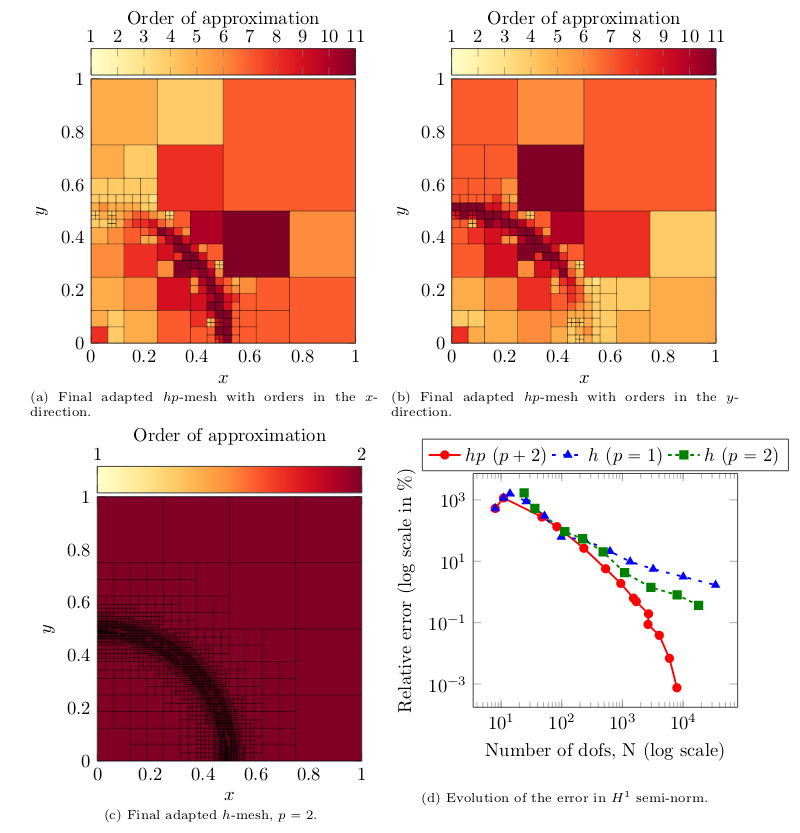
Together with the development of a posteriori estimators, a novel activity in the team is the design of efficient $hp$-adpative strategy. In this regard, we propose a multi-level hierarchical data structure imposing Dirichlet nodes to manage the so-called hanging nodes. Our $hp$-adaptive strategy is based on performing quasi-optimal unrefinements. Taking advantage of the hierarchical structure of the basis functions both in terms of the element size $h$ and the polynomial order of approximation $p$, we mark those with the lowest contributions to the energy of the solution and remove them. This straightforward unrefinement strategy does not require from a fine grid or complex data structures, making the algorithm flexible to many practical situations and existing implementations. Our first contribution has been recently submitted [42], and deals with the Poisson equation. Fig. 7 shows how the algorithm is able to correctly refine the computational grid to capture a shock wave.

Multiscale methods for frequency-domain wave propagation

Participants : Théophile Chaumont-Frelet, Zakaria Kassali, Stéphane Lanteri, Frédéric Valentin.

The design and analysis of multiscale methods for wave propagation is an important research line for team. The team actually mainly specializes in one family of multiscale methods, called multiscale hybrid-mixed (MHM). These developments started thanks to the close collaboration with Frédéric Valentin, who has recently been awarded an Inria international chair. Previous investigations in the context of this collaboration focused on time-dependent Maxwell's equations [10]. Recent efforts have been guided towards the realization of a MHM method for time-harmonic Maxwell's equations. We first focused on the Helmholtz equation, that modelizes the particular case of polarized waves. Our first results include the implementation of the method for two-dimensional problems as well as rigorous, frequency-explicit, stability and convergence analysis. These findings have recently been accepted for publication [40]. In the context of the internship of Zakaria Kassali, the method has been further adapted for the propagation of polarized waves in solar cells. Specifically, it is required in this case to take into account “quasi-periodic” boundary conditions that deserve a special treatment. We are currently undertaking further developments guided toward full three-dimensional Maxwell's equations with the PhD of Zakaria Kassali, which started in November 2019.