Section: New Results

Pluri-disciplinary Research

Biological Sequence Modeling with Convolutional Kernel Networks

Participants : Dexiong Chen, Laurent Jacob, Julien Mairal.

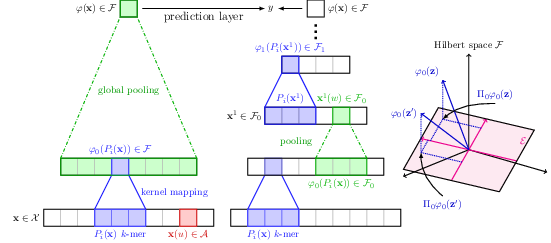
The growing number of annotated biological sequences available makes it possible to learn genotype-phenotype relationships from data with increasingly high accuracy. When large quan- tities of labeled samples are available for training a model, convolutional neural networks can be used to predict the phenotype of unannotated sequences with good accuracy. Unfortunately, their performance with medium- or small-scale datasets is mitigated, which requires inventing new data-efficient approaches. In this paper [4], [14], we introduce a hybrid approach between convolutional neural networks and kernel methods to model biological sequences. Our method, shown in Figure 17, enjoys the ability of convolutional neural networks to learn data representations that are adapted to a specific task, while the kernel point of view yields algorithms that perform significantly better when the amount of training data is small. We illustrate these advantages for transcription factor binding prediction and protein homology detection, and we demonstrate that our model is also simple to interpret, which is crucial for discovering predictive motifs in sequences. The source code is freely available at https://gitlab.inria.fr/dchen/CKN-seq.

Recurrent Kernel Networks

Participants : Dexiong Chen, Laurent Jacob [CNRS, LBBE Laboratory] , Julien Mairal.

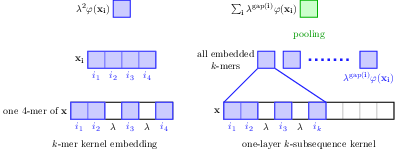
Substring kernels are classical tools for representing biological sequences or text. However, when large amounts of annotated data are available, models that allow end-to-end training such as neural networks are often preferred. Links between recurrent neural networks (RNNs) and substring kernels have recently been drawn, by formally showing that RNNs with specific activation functions were points in a reproducing kernel Hilbert space (RKHS). In this paper [15], we revisit this link by generalizing convolutional kernel networks—–originally related to a relaxation of the mismatch kernel—–to model gaps in sequences. It results in a new type of recurrent neural network (Figure 18), which can be trained end-to-end with backpropagation, or without supervision by using kernel approximation techniques. We experimentally show that our approach is well suited to biological sequences, where it outperforms existing methods for protein classification tasks.

Depth-adaptive Transformer

Participants : Maha Elbayad, Jiatao Gu [Facebook AI] , Edouard Grave [Facebook AI] , Michael Auli [Facebook AI] .

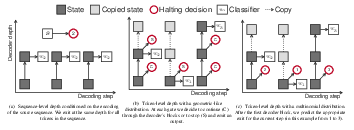
State of the art sequence-to-sequence models for large scale tasks perform a fixed number of computations for each input sequence regardless of whether it is easy or hard to process. In our ICLR'2020 paper [18], we train Transformer models which can make output predictions at different stages of the network and we investigate different ways to predict how much computation is required for a particular sequence. Unlike dynamic computation in Universal Transformers, which applies the same set of layers iteratively, we apply different layers at every step to adjust both the amount of computation as well as the model capacity. On IWSLT German-English translation our approach matches the accuracy of a well tuned baseline Transformer while using less than a quarter of the decoder layers. Figure 19 illustrates the different halting mechanisms investigated in this work. Namely, a sequence-level approach where we assume all the sequence's tokens are equally difficult and a token-level approach where tokens exit at varying depths.