Section: New Results

Synthesis of compact multiplexers and de-embedding of multiplexers

Participants : Martine Olivi, Fabien Seyfert, Stéphane Bila [Xlim, Limoges, France] , Hussein Ezzedin [Xlim, Limoges, France] , Damien Pacaud [Thales Alenia Space, Toulouse, France] , Giuseppe Macchiarella [Politecnico di Milano, Milan, Italy] , Matteo Oldoni [Politecnico di Milano, Milan, Italy] .

Synthesis of compact multiplexers

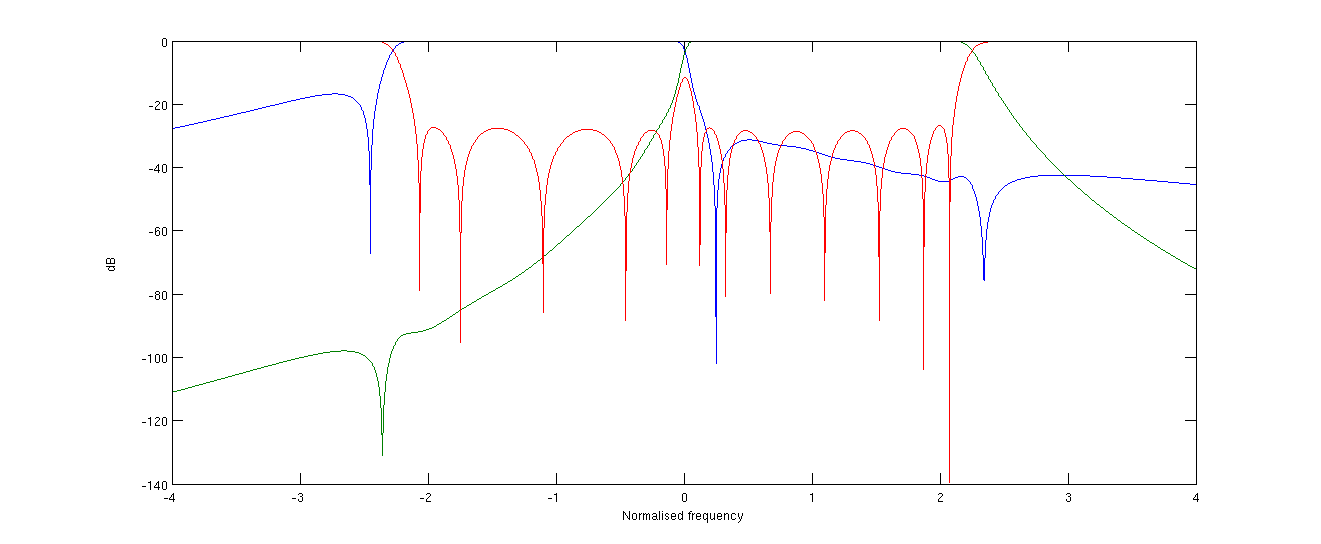
Our work on the synthesis problem for diplexers has continued this year. Based on the polynomial structure highlighted last year [39] , a synthesis algorithm was devised and allowed the effective synthesis of multiplexer characteristics (see figure 5 ). As opposed to other synthesis algorithms [74] the latter only involves polynomial computations on the sub-filters of the overall multiplexer, allowing its application to synthesis problems relative to devices with a numerous number of ports. The latter is based on the recursive solving of an extended Nevanlinna-Pick problem, first introduced in [62] . The convergence of this fixed point procedure is under study as well as its extension to the synthesis of general multiplexer.

Figure 5. Diplexer's characteristic computed with an algorithm based on the recursive solving of extended Nevanlinna-Pick interpolation problems.

De-embedding of multiplexers

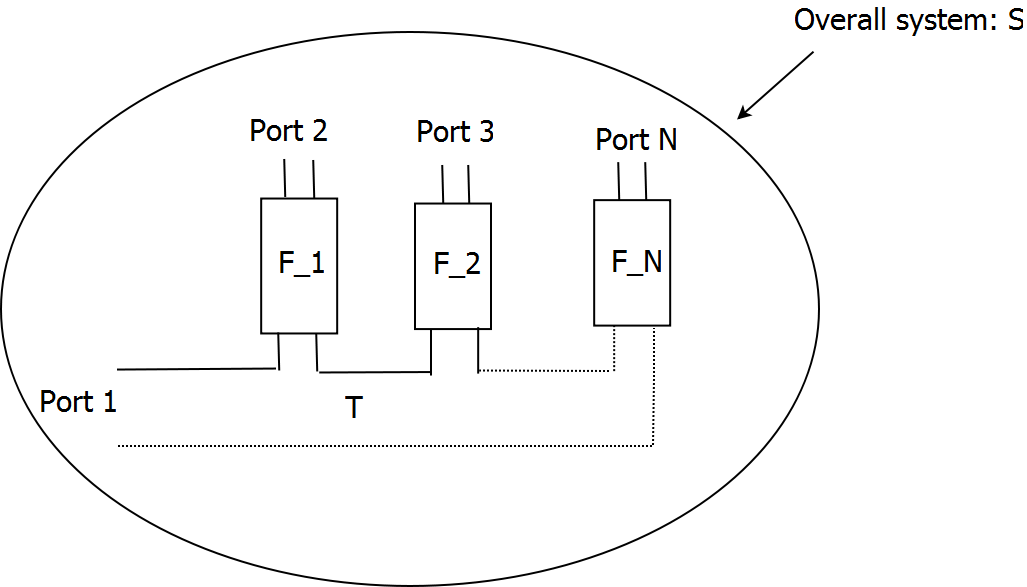
While we presented our work on the de-embedding diplexers at [26] we extended the latter to general multiplexers. The multiplexer de-embedding problem we study is the following. Let $S$ be the measured scattering matrix of a multiplexer composed of a $N$-port junction with response $T$ and $N-1$ filtering devices with responses $F_1,\cdots F_{N-1}$ as depicted by Figure 6 .

Figure 6. Multiplexer made of a junction $T$ and filtering devices $F_1,F_2\cdots F_N$.

The de-embedding question is the following: given $S$ and $T$, is it possible to derive the $F_k$'s ? We derived some rather important and surprising characteristics of this general problem:

• When stating the de-embedding problem in terms of chain rather that scattering matrices, the latter becomes linear,

• For a generic junction the de-embedding problem has a unique solution for $N=2$ and $N>3$ while it is degenerated for $N=3$,

• Degeneracy depends on the junction's response and can be explained by the occurence of filtering responses that hide behind the junction. These are responses $F_1,\cdots F_{N-1}$ such that when chained to the junction, the response $T$ remains unchanged.

In the light of these theoretical results the tractability of the practical problem is currently under investigation. For example, it appears that in practice the $T$ responses can not be considered as generic as they are often build by chaining several 3-junctions together. Moreover, while theoretically uniqueness of the de-embedding solution seems to be guaranteed for large values of $N$, the sensitivity of the latter with respect to measurements errors grows dramatically with $N$. Therefore approaches that entail additional hypotheses, such as rationality of the responses $F_k$ are being studied. This work is pursued in collaboration with Thales Alenia Space and the Politecnico di Milano.