Section: Application Domains

Identification and design of microwave devices

Participants : Laurent Baratchart, Sylvain Chevillard, Martine Olivi, Fabien Seyfert.

This work is done in collaboration with Stéphane Bila (XLim, Limoges) and Jean-Paul Marmorat (Centre de mathématiques appliquées (CMA), École des Mines de Paris).

One of the best training grounds for the research of the team in function theory is the identification and design of physical systems for which the linearity assumption works well in the considered range of frequency, and whose specifications are made in the frequency domain. This is the case of electromagnetic resonant systems which are of common use in telecommunications.

In space telecommunications (satellite transmissions), constraints specific to on-board technology lead to the use of filters with resonant cavities in the microwave range. These filters serve multiplexing purposes (before or after amplification), and consist of a sequence of cylindrical hollow bodies, magnetically coupled by irises (orthogonal double slits). The electromagnetic wave that traverses the cavities satisfies the Maxwell equations, forcing the tangent electrical field along the body of the cavity to be zero. A deeper study (of the Helmholtz equation) states that essentially only a discrete set of wave vectors is selected. In the considered range of frequency, the electrical field in each cavity can be seen as being decomposed along two orthogonal modes, perpendicular to the axis of the cavity (other modes are far off in the frequency domain, and their influence can be neglected).

Figure 1. Picture of a 6-cavities dual mode filter. Each cavity (except the last one) has 3 screws to couple the modes within the cavity, so that 16 quantities must be optimized. Quantities such as the diameter and length of the cavities, or the width of the 11 slits are fixed during the design phase.

Each cavity (see Figure 1 ) has three screws, horizontal, vertical and midway (horizontal and vertical are two arbitrary directions, the third direction makes an angle of 45 or 135 degrees, the easy case is when all cavities show the same orientation, and when the directions of the irises are the same, as well as the input and output slits). Since the screws are conductors, they act more or less as capacitors; besides, the electrical field on the surface has to be zero, which modifies the boundary conditions of one of the two modes (for the other mode, the electrical field is zero hence it is not influenced by the screw), the third screw acts as a coupling between the two modes. The effect of the iris is to the contrary of a screw: no condition is imposed where there is a hole, which results in a coupling between two horizontal (or two vertical) modes of adjacent cavities (in fact the iris is the union of two rectangles, the important parameter being their width). The design of a filter consists in finding the size of each cavity, and the width of each iris. Subsequently, the filter can be constructed and tuned by adjusting the screws. Finally, the screws are glued. In what follows, we shall consider a typical example, a filter designed by the CNES in Toulouse, with four cavities near 11 Ghz.

Near the resonance frequency, a good approximation of the Maxwell equations is given by the solution of a second order differential equation. One obtains thus an electrical model for our filter as a sequence of electrically-coupled resonant circuits, and each circuit will be modelled by two resonators, one per mode, whose resonance frequency represents the frequency of a mode, and whose resistance represent the electric losses (current on the surface).

In this way, the filter can be seen as a quadripole, with two ports, when plugged on a resistor at one end and fed with some potential at the other end. We are then interested in the power which is transmitted and reflected. This leads to defining a scattering matrix $S$, that can be considered as the transfer function of a stable causal linear dynamical system, with two inputs and two outputs. Its diagonal terms $S_{1,1}$, $S_{2,2}$ correspond to reflections at each port, while $S_{1,2}$, $S_{2,1}$ correspond to transmission. These functions can be measured at certain frequencies (on the imaginary axis). The filter is rational of order 4 times the number of cavities (that is 16 in the example), and the key step consists in expressing the components of the equivalent electrical circuit as a function of the $S_{ij}$ (since there are no formulas expressing the lengths of the screws in terms of parameters of this electrical model). This representation is also useful to analyze the numerical simulations of the Maxwell equations, and to check the design, particularly the absence of higher resonant modes.

In fact, resonance is not studied via the electrical model, but via a low-pass equivalent circuit obtained upon linearising near the central frequency, which is no longer conjugate symmetric (i.e. the underlying system may not have real coefficients) but whose degree is divided by 2 (8 in the example).

In short, the identification strategy is as follows:

• measuring the scattering matrix of the filter near the optimal frequency over twice the pass band (which is 80Mhz in the example).

• Solving bounded extremal problems for the transmission and the reflection (the modulus of he response being respectively close to 0 and 1 outside the interval measurement, cf. section  3.3.1 ). This provides us with a scattering matrix of order roughly 1/4 of the number of data points.

• Approximating this scattering matrix by a rational transfer-function of fixed degree (8 in this example) via the Endymion or RARL2 software (cf. section  3.3.2.2 ).

• A realization of the transfer function is thus obtained, and some additional symmetry constraints are imposed.

• Finally one builds a realization of the approximant and looks for a change of variables that eliminates non-physical couplings. This is obtained by using algebraic-solvers and continuation algorithms on the group of orthogonal complex matrices (symmetry forces this type of transformation).

Figure 2. Nyquist Diagram. Rational approximation (degree 8) and data - $S_{22}$.

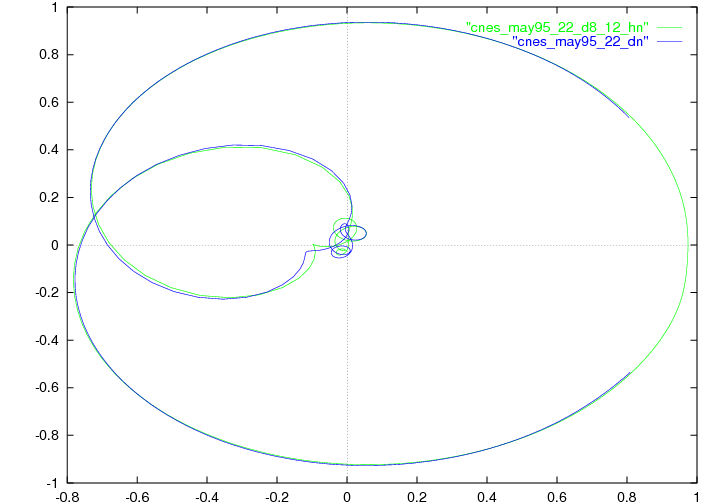
The final approximation is of high quality. This can be interpreted as a validation of the linearity hypothesis for the system: the relative $L^2$ error is less than ${10}^{-3}$. This is illustrated by a reflection diagram (Figure 2 ). Non-physical couplings are less than ${10}^{-2}$.

The above considerations are valid for a large class of filters. These developments have also been used for the design of non-symmetric filters, useful for the synthesis of repeating devices.

The team also investigates problems relative to the design of optimal responses for microwave devices. The resolution of a quasi-convex Zolotarev problems was for example proposed, in order to derive guaranteed optimal multi-band filter's responses subject to modulus constraints [11] . This generalizes the classical single band design techniques based on Tchebychev polynomials and elliptic functions. These techniques rely on the fact that the modulus of the scattering parameters of a filters, say $|S_{1,2}|$, admits a simple expression in terms of the filtering function $D=|S_{1,1}|/|S_{1,2}|$ namely,

The filtering function appears to be the ratio of two polynomials $p_1/p_2$, the numerator of the reflection and transmission scattering factors, that can be chosen freely. The denominator $q$ is obtained as the unique stable and unitary polynomial solving the classical Feldtkeller spectral equation:

The relative simplicity of the derivation of filter's responses under modulus constraints is due to this ability to "forget" about latter spectral equation, and express all design constraints on the filtering functions $D$. This no longer the case when considering the synthesis $N$-port devices for $N>3$, like multiplexers, routers power dividers or when considering the synthesis of filters under matching conditions. The efficient derivation of multiplexers responses is one of the team's active recent research area, where technique based on constrained Nevanlinna-Pick interpolation problems are under study (see section 6.4.1 ).