Section: New Results

Singularity analysis and reconstructible systems

Participants : Oriol Pont [correspondant] , Hussein Yahia, Antonio Turiel.

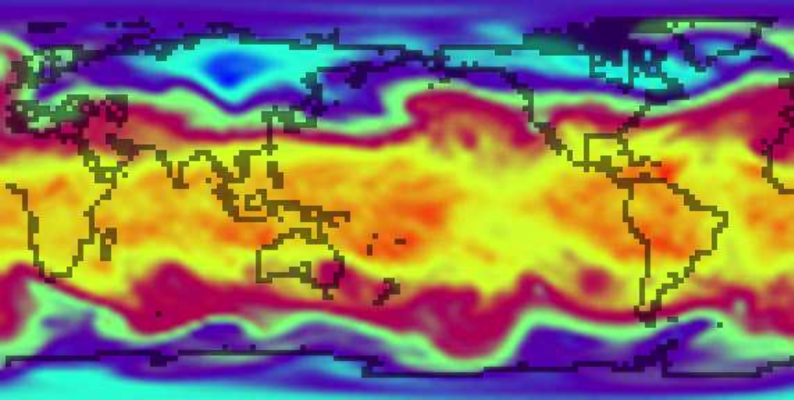
The local singularity exponents of a signal are directly related to the distribution of information in it. This fact implies that accurate evaluation of such exponents opens the door to signal reconstruction and characterisation of the dynamical parameters of the process originating the signal. Many practical implications arise in a context of digital signal processing, since the information on singularity exponents is usable for compact encoding, reconstruction and inference. The evaluation of singularity exponents in a digital context is not straightforward and requires the calculation of the Unpredictable Point Manifold of the signal. In this work, we present an algorithm for estimating the values of singularity exponents at every point of a digital signal of any dimension. We show that the key ingredient for robust and accurate reconstructibility performance lies on the definition of multiscale measures in the sense that they encode the degree of singularity and the local predictability at the same time. See figure 7 .

Figure 7. Left: 876576th hour slice of ERA-40 artificially rescaled 4x with bicubic interpolation for the purpose of clarity of illustration. Middle: singularity exponents calculated only in the space. Some rescaling artefacts visibly appear but without significant disturbance of the fine structure details. Right: singularity exponents calculated in the space-time domain. Notice the increased degree of detail when the temporal information is taken into account.

• Related publication: [13] .