Section: New Results
Image assimilation
Sequences of images, such as satellite acquisitions, display structures evolving in time. This information is recognized of major interest by forecasters (meteorologists, oceanographers, etc.) in order to improve the information provided by numerical models. However, these satellite images are mostly assimilated in geophysical models on a point-wise basis, discarding the space-time coherence visualized by the evolution of structures such as clouds. Assimilating in an optimal way image data is of major interest and this issue should be considered in two ways:
-
from the model's viewpoint, the location of structures on the observations is used to control the state vector.
-
from the image's viewpoint, a model of the dynamics and structures is built from the observations.
Divergence-free motion estimation
Participants : Dominique Béréziat [UPMC] , Isabelle Herlin, Sergiy Zhuk [IBM Research, Ireland] .
This research addresses the issue of divergence-free motion estimation on an image sequence, acquired over a given temporal window. Unlike most state-of-the-art technics, which constrain the divergence to be small thanks to Tikhonov regularization terms, a method that imposes a null value of divergence of the estimated motion is defined.
Motion is either characterized by its vorticity value or by its coefficients on a divergence-free basis and assumed to satisfy the Lagragian constancy hypothesis. An image assimilation method, based on the 4D-Var technic, is defined that estimates motion as a compromise between the evolution equations of vorticity or projection coefficients and the observed sequence of images.
The method is applied on Sea Surface Temperature (SST) images acquired over Black Sea by NOAA-AVHRR sensors. The divergence-free assumption is roughly valid on these acquisitions, due to the small values of vertical velocity at the surface.
Model error and motion estimation
Participants : Dominique Béréziat [UPMC] , Isabelle Herlin.
Data assimilation technics are used to retrieve motion from image sequences. These methods require a model of the underlying dynamics, displayed by the evolution of image data. In order to quantify the approximation linked to the chosen dynamic model, an error term is included in the evolution equation of motion and a weak formulation of 4D-Var data assimilation is designed. The cost function to be minimized simultaneously depends on the initial motion field, at the begining of the studied temporal window, and on the error value at each time step. The result allows to assess the model error and analyze its impact on motion estimation.
The approach has been used to estimate the impact of geophysical forces (gravity, Coriolis, diffusion) and better assess the surface dynamics [24] .
Tracking of structures from an image sequence
Participants : Yann Lepoittevin, Isabelle Herlin, Dominique Béréziat [UPMC] .
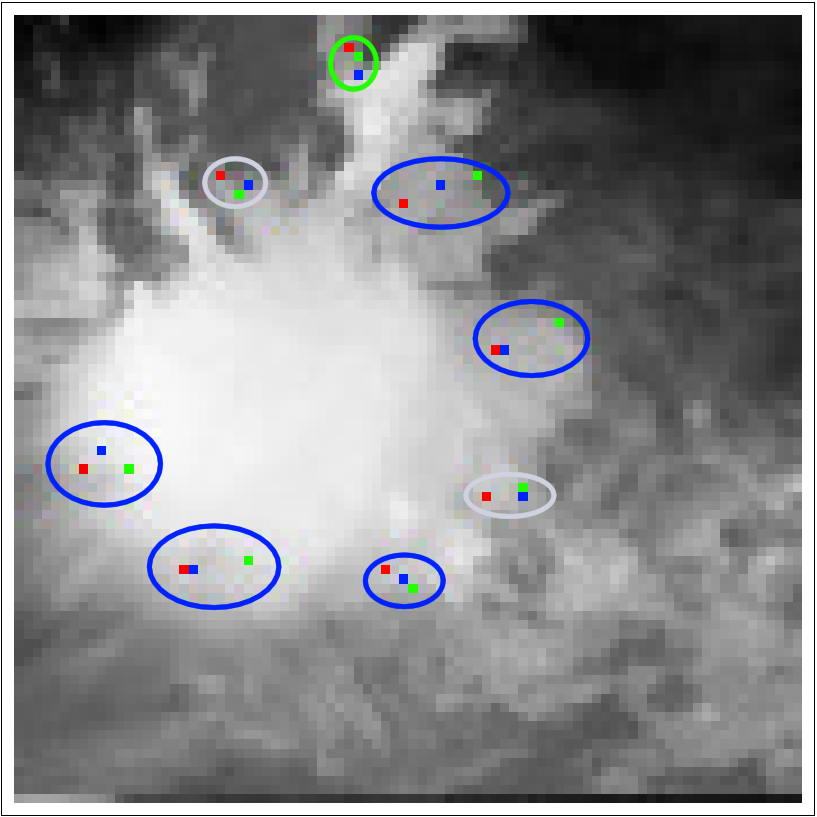
The research concerns an approach to estimate velocity on an image sequence and simultaneously segment and track a given structure. It relies on the underlying dynamics' equations of the studied physical system. A data assimilation method is designed to solve evolution equations of image brightness, those of motion's dynamics, and those of the distance map modeling the tracked structures. The method is applied on meteorological satellite data, in order to track tropical clouds on image sequences and estimate their motion, as seen on Fig. 3 .
Quantification is obtained on synthetic experiments by comparing trajectories of characteristic points. The respective position of these points on the last image of the sequence for different methods may be compared to that obtained with ground truth as seen on Fig. 4 .
|
Data assimilation is performed either with a 4D-Var variational approach [27] , [30] , [28] or with an ensemble approach. In the last case, computation of the ensemble from optical flow methods of the literature is currently studied.