Section: New Results

Minimax filtering

In minimax filtering for state estimation, the initial state error, the model error and the observation errors are supposed to belong to one joint ellipsoid. It is only assumed that the errors, stochastic or deterministic, are bounded. During the assimilation process, the filter computes an ellipsoid where one will find at least all states compatible with observations and errors description. The state estimate is taken as the center of the ellipsoid. No assumption on the actual distribution of the errors in needed and the state estimate minimizes the worst-case error, which makes the filter robust.

Retrieval of a continuous image function and a posteriori minimax motion estimation

Participants : Sergiy Zhuk [IBM Research, Ireland] , Isabelle Herlin, Olexander Nakonechnyi [Taras Shevchenko National University of Kyiv] , Jason Frank [CWI, the Netherlands] .

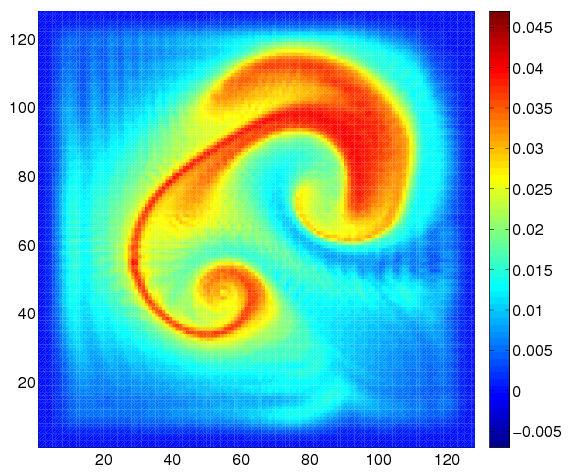
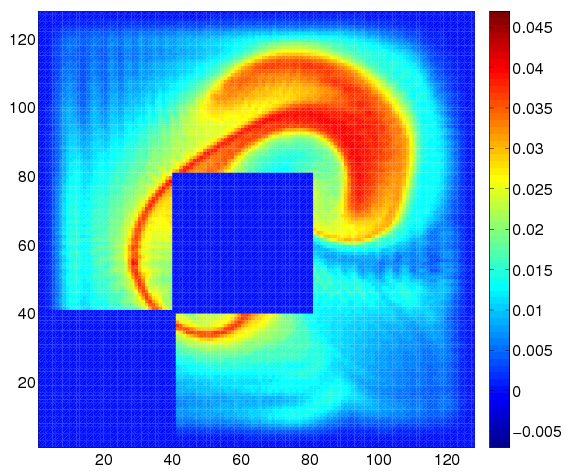
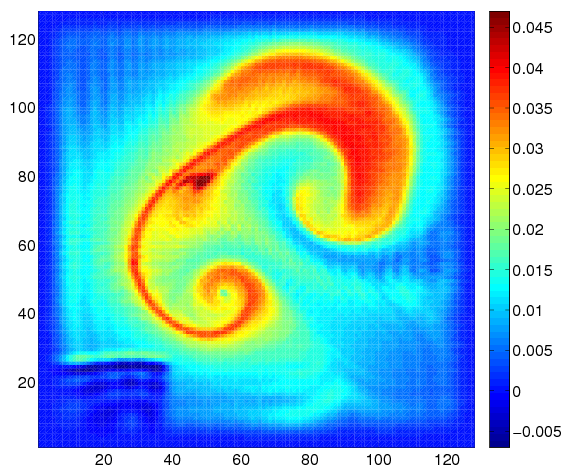
An iterative minimax method is developed for the problem of motion estimation from an image sequence. The main idea of the algorithm is to use the "bi-linear" structure of the Navier-Stokes equations and optical flow constraint in order to iteratively estimate the velocity. The algorithm consists of the following parts:

1) we construct a continuous image function $\widehat{I}$, solving the optical flow constraint, such that $\widehat{I}$ fits (in the sense of least-squares) the observed sequence of images. To do so, we set the velocity field in the optical flow constraint to be the current minimax estimate of the velocity field $𝐰$, obtained at the previous iteration of the algorithm, and construct the minimax estimate $\widehat{I}$ of the resulting linear advection equation using the observed image sequence as discrete measurements of the brightness function;

2) we plug the estimate of the image gradient, obtained out of pseudo-observations $\widehat{I}$ in 1), into the optical flow constraint and the current minimax estimate $𝐰$ of the velocity field into the non linear part of Navier-Stokes equations so that we end up with a system of linear PDEs, which represents an extended state equation: it contains a linear parabolic equation for the velocity field and linear advection equation for the image brightness function. We construct the minimax estimate of the velocity field from the extended state equation using again the observed image sequence as discrete measurements of the brightness function;

3) we use the minimax estimate of the velocity field obtained in 2) in order to start 1) again.

Alternatively, point 1) may be used to retrieve a continuous image function from sparse and noisy image snapshots, based on previous motion estimation with a 4D-Var technic as seen on Fig. 5 , that displays ground truth, noisy image observation, image estimation at the end of the studied intervall.