Section: New Results
Applications of deterministic optimal control problems
Optimization of running strategies based on anaerobic energy and variations of velocity
Participant : Joseph Frédéric Bonnans.
In the report [29] we present new models, numerical simulations and rigorous analysis for the optimization of the velocity in a race. In a seminal paper, Keller [74] , [75] explained how a runner should determine his speed in order to run a given distance in the shortest time. We extend this analysis, based on the equation of motion and aerobic energy, to include a balance of anaerobic energy (or accumulated oxygen deficit) and an energy recreation term when the speed decreases. We also take into account that when the anaerobic energy gets too low, the oxygen uptake cannot be maintained to its maximal value. Using optimal control theory, we obtain a proof of Keller's optimal race, and relate the problem to a relaxed formulation, where the propulsive force represents a probability distribution rather than a value function of time. Our analysis leads us to introduce a bound on the variations of the propulsive force to obtain a more realistic model which displays oscillations of the velocity. Our numerical simulations qualitatively reproduce quite well physiological measurements on real runners. We show how, by optimizing over a period, we recover these oscillations of speed. We point out that our numerical simulations provide in particular the exact instantaneous anaerobic energy used in the exercise.
Optimal control of leukemic cell population dynamics
Participant : Xavier Dupuis.
In the paper [33] we discuss the optimal co-administration of two drugs for some acute myeloid leukemias (AML), and we are looking for in vitro protocols as a first step. This issue can be formulated as an optimal control problem. The dynamics of leukemic cell populations in culture is given by age-structured partial differential equations, which can be reduced to a system of delay differential equations, and where the controls represent the action of the drugs. The objective function relies on eigenelements of the uncontrolled model and on general relative entropy, with the idea to maximize the efficiency of the protocols. The constraints take into account the toxicity of the drugs. We present in this paper the modeling aspects, as well as theoretical and numerical results on the optimal control problem that we get.
Contrast imaging problem in nuclear magnetic resonance
Participant : Pierre Martinon.
In collaboration with team McTAO (Sophia), we studied in [25] and [36] the contrast imaging problem in nuclear magnetic resonance, modeled as Mayer problem in optimal control. The optimal solution can be found as an extremal, solution of the Maximum Principle and analyzed with the techniques of geometric control. A first synthesis of locally optimal solutions is given in the single-input case, with some preliminary results in the bi-input case. We conducted a comprehensive numerical investigation of the problem, using a combination of indirect shooting (HamPath software) and direct method (Bocop ), with a moment-based (LMI ) technique to estimate the global optimum.
Optimizing the anaerobic digestion of microalgae in a coupled process
Participant : Pierre Martinon.
In collaboration with the Inra-Inria team MODEMIC (Montpellier), we studied in [30] a bio-reactor system describing the coupling of a culture of micro-algae and an anaerobic digester. Our aim is to optimize the production of methane in the digester during a certain number of days with respect to the dilution rate (the input flow of micro-algae in the digester). The mathematical model for the dynamics of the two reactors takes into account a periodic day-night model of the light in the culture of micro-algae, and a chemostat model for the digester. We first prove existence and attraction of periodic solutions for a one day period, and we apply Pontryagin's Maximum Principle (PMP) in order to characterize optimal controls. We provide numerical simulations for different light models, by a direct method that we refine using an indirect shooting. We also investigate the dependence of the optimal cost with respect to the ratio of the volumes of the two tanks. Finally, we investigate the optimal strategies over a large number of days without periodic constraints, and compared the mean cost to the optimal cost over one period.
Design of optimal experiments for parameter estimation of microalgae growth models
Participant : Pierre Martinon.
In collaboration with team BIOCORE (Sophia), we investigated in [27] techniques of Optimal Experiment Design for microalgae growth models. In order to have microalgae growth models that are useful for prediction and process optimization, reliable parameters need to be provided. This reliability implies a careful design of experiments that can be exploited for parameter estimation. OED techniques can provide guidelines for the design of experiments with high informative content that allow an accurate parameter estimation. We study a real experimental device devoted to evaluate the effect of temperature and light on microalgae growth. On the basis of a mathematical model of the experimental system, the optimal experiment design problem was solved as an optimal control problem. E-optimal experiments were obtained by using two discretization approaches, namely sequential and simultaneous. The results showed that an adequate parameterization of the experimental inputs provided optimal solutions very close to those provided by the simultaneous discretization. Simulation results showed the relevance of determining optimal experimental inputs for achieving an accurate parameter estimation.
Controllability and optimal strokes for N-link microswimmer
Participant : Pierre Martinon.
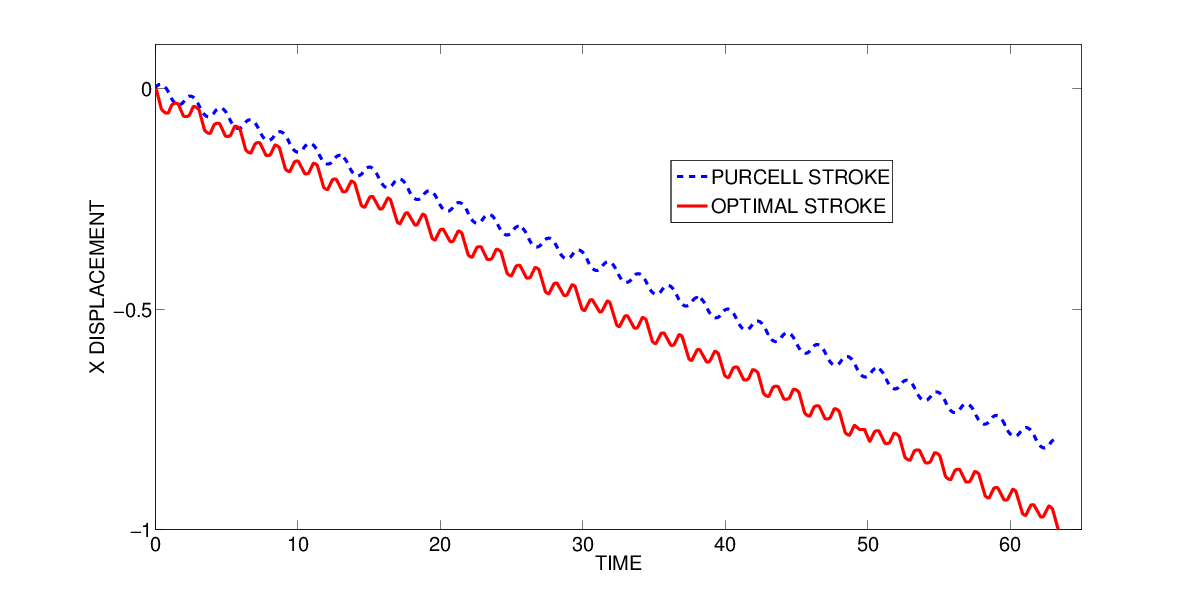
In [39] we focus on the N-link swimmer, a generalization of the classical Purcell swimmer. We use the simplification of the Resistive Force Theory to derive the motion equation for the swimmer in a fluid with a low Reynolds number. We prove that the swimmer is controllable in the whole plane when it is composed by more than 3 sticks and for almost every set of stick lengths. As a direct result, we show that there exists an optimal swimming strategy which leads to minimize the time to reach a desired configuration. Numerical experiments on the case of the Purcell swimmer suggest that the optimal strategy is periodic, i.e. composed of a sequence of identical strokes. Our results indicate that this candidate for an optimal stroke indeed gives a better speed than the classical Purcell stroke. Future directions for this work include the design of robotic micro-swimmers, as well as investigation of the movement of swimming micro-organisms.