Section: Application Domains

Computational geoseismics

Computational challenges in geoseismics span a wide range of disciplines and have significant scientific and societal implications. Two important topics are mitigation of seismic hazards and discovery of economically recoverable petroleum resources. The research activities of the NACHOS project-team in this domain before all focus on the development of numerical methodologies and simulation tools for seismic hazard assessment, while the involvement on the second topic has been been intiated recently.

Seismic hazard assessment.

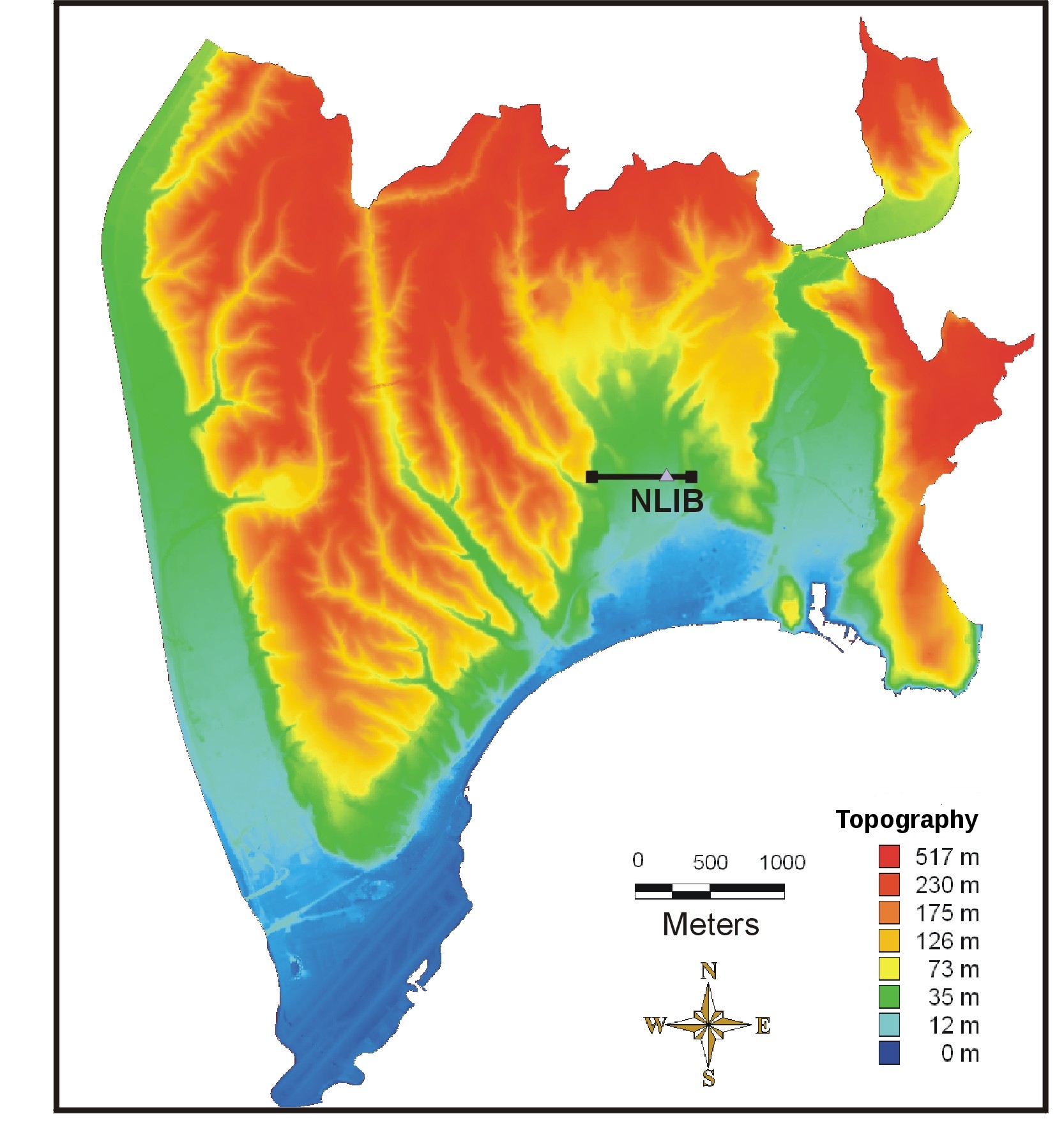
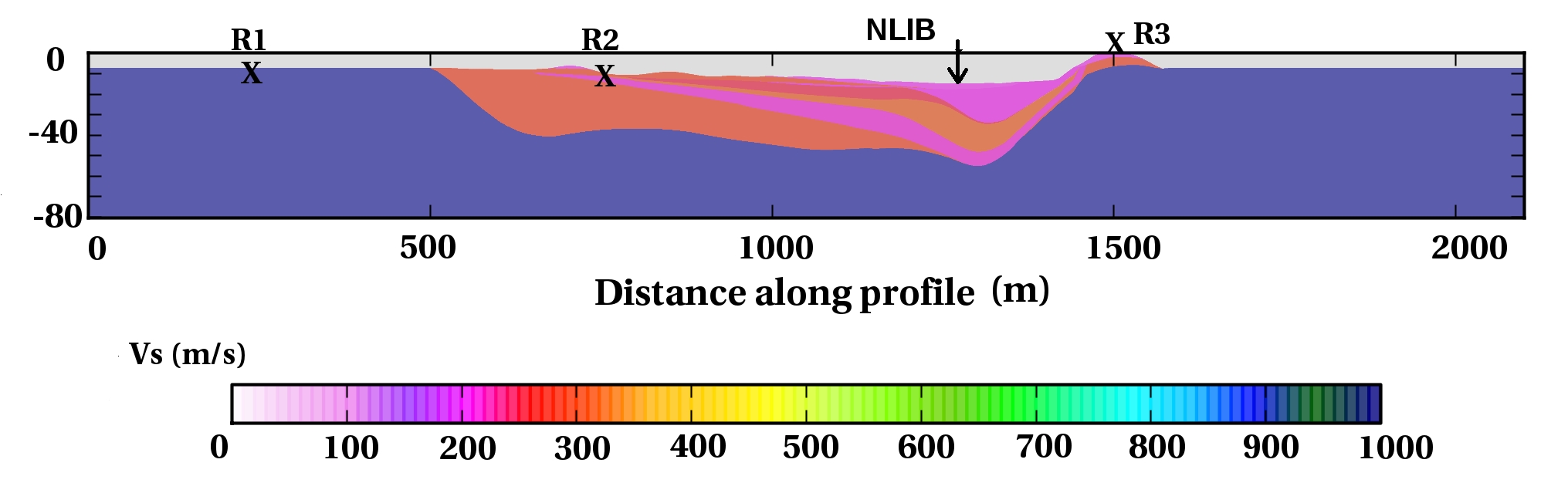
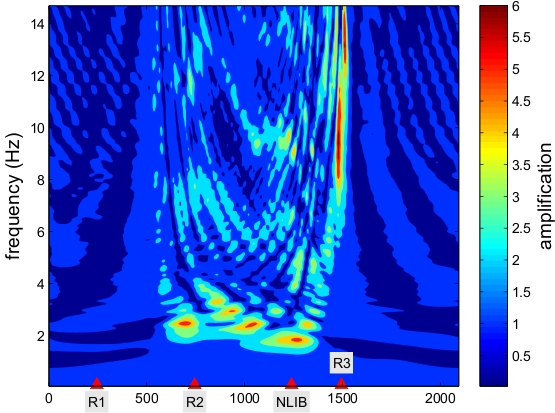
To understand the basic science of earthquakes and to help engineers better prepare for such an event, scientists want to identify which regions are likely to experience the most intense shaking, particularly in populated sediment-filled basins. This understanding can be used to improve building codes in high hazard areas and to help engineers design safer structures, potentially saving lives and property. In the absence of deterministic earthquake prediction, forecasting of earthquake ground motion based on simulation of scenarios is one of the most promising tools to mitigate earthquake related hazard. This requires intense modeling that meets the spatial and temporal resolution scales of the continuously increasing density and resolution of the seismic instrumentation, which record dynamic shaking at the surface, as well as of the basin models. Another important issue is to improve the physical understanding of the earthquake rupture processes and seismic wave propagation. Large scale simulations of earthquake rupture dynamics and wave propagation are currently the only means to investigate these multi-scale physics together with data assimilation and inversion. High resolution models are also required to develop and assess fast operational analysis tools for real time seismology and early warning systems. Modeling and forecasting earthquake ground motion in large basins is a challenging and complex task. The complexity arises from several sources. First, multiple scales characterize the earthquake source and basin response: the shortest wavelengths are measured in tens of meters, whereas the longest measure in kilometers; basin dimensions are on the order of tens of kilometers, and earthquake sources up to hundreds of kilometers. Second, temporal scales vary from the hundredths of a second necessary to resolve the highest frequencies of the earthquake source up to as much as several minutes of shaking within the basin. Third, many basins have a highly irregular geometry. Fourth, the soil's material properties are highly heterogeneous. And fifth, geology and source parameters are observable only indirectly and thus introduce uncertainty in the modeling process. Because of its modeling and computational complexity, earthquake simulation is currently recognized as a grand challenge problem.

Numerical methods for the propagation of seismic waves have been studied for many years. Most of existing numerical software rely on finite difference type methods. Among the most popular schemes, one can cite the staggered grid finite difference scheme proposed by Virieux [62] and based on the first order velocity-stress hyperbolic system of elastic waves equations, which is an extension of the scheme derived by Yee [63] for the solution of the Maxwell equations. Many improvements of this method have been proposed, in particular, higher order schemes in space or rotated staggered-grids allowing strong fluctuations of the elastic parameters. Despite these improvements, the use of cartesian grids is a limitation for such numerical methods especially when it is necessary to incorporate surface topography or curved interface. Moreover, in presence of a non planar topography, the free surface condition needs very fine grids (about 60 points by minimal Rayleigh wavelength) to be approximated. In this context, our objective is to develop high order unstructured mesh based methods for the numerical solution of the system of elastodynamic equations for elastic media in a first step, and then to extend these methods to a more accurate treatment of the heterogeneities of the medium or to more complex propagation materials such as viscoelastic media which take into account the intrinsic attenuation. Initially, the team has considered in detail the necessary methodological developments for the large-scale simulation of earthquake dynamics [2] -[1] . More recently, the team has initiated a close collaboration with CETE Méditerranée http://www.cete-mediterranee.fr/gb which is a regional technical and engineering centre whose activities are concerned with seismic hazard assessment studies, and IFSTTAR http://www.ifsttar.fr/en/welcome which is the French institute of science and technology for transport, development and networks, conducting research studies on control over aging, risks and nuisances.

Imperfect interfaces.

A long term scientific collaboration (at least 5 years long) has been recently set up between the NACHOS project-team and LMA (Laboratoire de Mécanique et Acoustique) http://www.lma.cnrs-mrs.fr with the arrival of Marie-Hélène Lallemand who joigned NACHOS in October 2012. That collaboration has been motivated by common scientific interests concerning both geodynamics (seismic wave propagation) and seismology (Non Destructive Control by wave propagation). The goal is to contribute in the area of both fracture dynamics modelings and the setting of adequate constitutive laws for interfaces separating two continuous media. Since the whole medium under study is heterogeneous in term of both materials and geometries, the study of equivalent homogeneous representation/modellings is crucial to get a suitable reduced model which can be used for numerical simulations. In the particular example of rock-type soils near mountain areas, the medium may be viewed from the geologist, at the macro-scale, for example, as large layers of continuous materials separated by interfacial areas through which discontinuities (of displacements, velocities, stress components ...) may occur. Even if the so-called interfaces may have a depth which may attain many times ten meters and a length of many times hundred meters, they are assimilated as interfaces, from the geologist point of view. Inside those thin layers, there are usually some mixture of multiphase materials (water, sand, gas, etc.), and the exact composition is not known in advance. While perfect interfaces are usually assumed in inverse problems in sismology, the question is to qualify and to quantify the errors if we do not take those assumptions for granted. When soil rheology is requested, assuming perfect interfaces or imperfect interfaces greatly influence the physical parameters obtained in reversing the data collected in the captors. Interface modelling is one of the expertise area of LMA, and the project-team is interested in taking that opportunity to improve its knowledge in multi-scale modelling while ready to help answering the numerical implementation of such resulting models. That collaboration is not restricted to that aspect though. Well-posedness of the resulting models, numerical solvers are also domains which are also addressed.

Seismic exploration.

This application topic has been considered recently by the NACHOS project-team and this is done in close collaboration with the MAGIQUE-3D project-team at Inria Bordeaux - Sud-Ouest which is coordinating the Depth Imaging Partnership (DIP) http://dip.inria.fr between Inria and TOTAL. The research program of DIP includes different aspects of the modeling and numerical simulation of sesimic wave propagation that must be considered to construct an efficient software suites for producing accurate images of the subsurface. Our common objective with the MAGIQUE-3D project-team is to design high order unstructured mesh based methods for the numerical solution of the system of elastodynamic equations in the time domain and in the frequency domain, that will be used as forward modelers in appropriate inversion procedures.