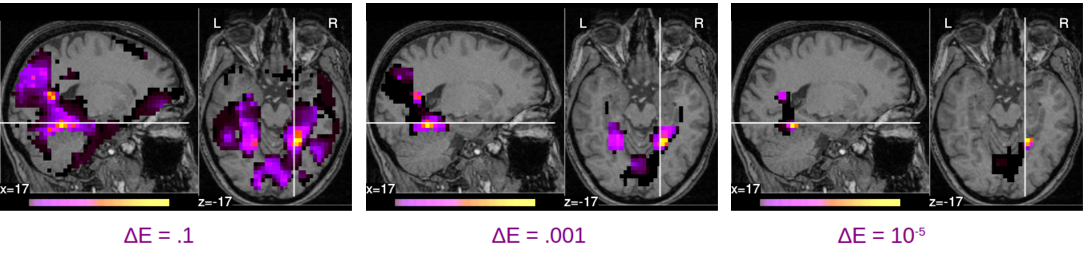
Section: New Results
Benchmarking solvers for TV-l1 least-squares and logistic regression in brain imaging
Participants : Elvis Dohmatob [correspondant] , Michael Eickenberg, Gaël Varoquaux, Bertrand Thirion.
Learning predictive models from brain imaging data, as in decoding cognitive states from fMRI (functional Magnetic Resonance Imaging), is typically an ill-posed problem as it entails estimating many more parameters than available sample points. This estimation problem thus requires regularization. Total variation regularization, combined with sparse models, has been shown to yield good predictive performance, as well as stable and interpretable maps. However, the corresponding optimization problem is very challenging: it is non-smooth, non-separable and heavily ill-conditioned. For the penalty to fully exercise its structuring effect on the maps, this optimization problem must be solved to a good tolerance, resulting in a computational challenge. In this work, we explore a wide variety of solvers and exhibit their convergence properties on fMRI data. We introduce a variant of smooth solvers and show that it is a promising approach in these settings. Our findings show that care must be taken in solving TV-l1 estimation in brain imaging and highlight the successful strategies.
|
More details can be found in [30]