Section: New Results

Patch-based statistical denoising methods for electron and light microscopy

Participants : Charles Kervrann, Frédéric Lavancier.

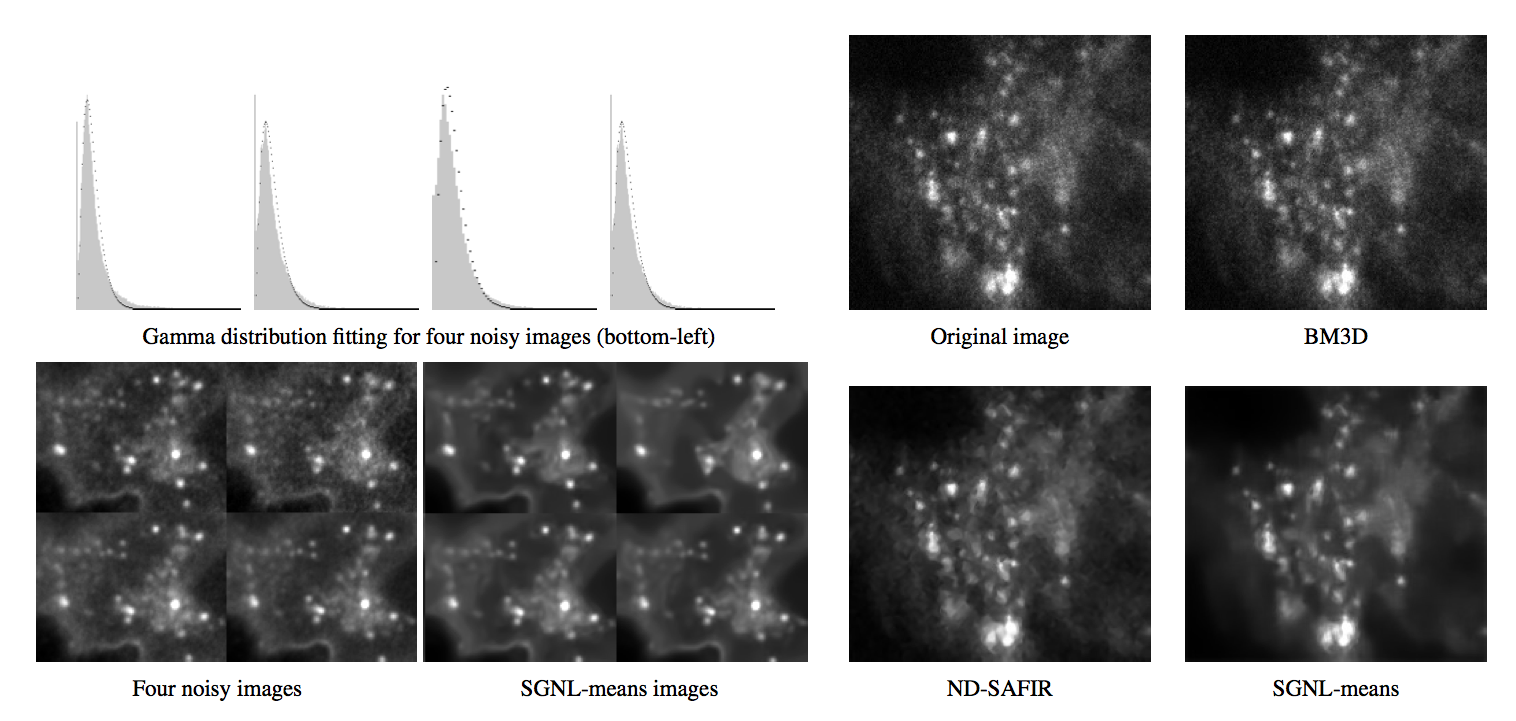
Inspired form the non-local means [33] , we developed a stochastic NL-means-based denoising algorithm for generalized non-parametric noise models [21] , [9] . First, we provided a statistical interpretation to current patch-based neighborhood filters and justify the Bayesian inference that needs to explicitly account for discrepancies between the model and the data. Furthermore, we investigated the Approximate Bayesian Computation (ABC) rejection method [30] , [46] combined with density learning techniques for handling situations where the posterior is intractable or too prohibitive to calculate. This is particularly relevant for images contaminated by heterogeneous sources of noise. A major difference with previous methods is that we directly handle the structure of the noise, without precise parametric modeling of the noise. We demonstrated the flexibility of our stochastic Gamma non-local means (SGNL-means) by showing how it can be adapted to tackle noise in frequency domain fluorescence lifetime imaging microscopy (FD-FLIM) and cryo-electron tomography (see Fig. 3 ).

Moreover, we also proposed a general statistical aggregation method which combines image patches denoised with several commonly-used algorithms [20] . We showed that weakly denoised versions of the input image obtained with standard methods, can serve to compute an efficient patch-based aggregated estimator. In our approach, we evaluate the Stein’s Unbiased Risk Estimator (SURE) of each denoised candidate image patch and use this information to compute the exponential weighted aggregation (EWA) estimator. The aggregation method is flexible enough to combine any standard denoising algorithm and has an interpretation with Gibbs distribution. The denoising algorithm (PEWA) is based on an MCMC sampling and is able to produce results that are comparable to the state of the art ([4] , [38] ). In this range of work, we have also introduced in [28] a general method to combine estimators in order to produce a better estimate. From a theoretical point of view, we proved that this method is optimal in some sense. It is illustrated on standard statistical problems in parametric and semi-parametric models where the averaging estimator outperforms the initial estimators in most cases. As part of an on-going work, we are applying this method to improve patch-based image denoising algorithms.

References:  [9] [21] [20] [28]

 

Collaborators: Philippe Roudot (UT Southwestern Medical Center, Dallas (TX))

                          Francois Waharte (UMR 144 CNRS-Institut Curie, STED team and PICT-IBiSA)

                          Paul Rochet (Laboratoire de Mathématiques Jean Leray (LMJL), university of Nantes)