Section: New Results
Uncertainty quantification and risk assessment
The uncertainty quantification of environmental models raises a number of problems due to:
-
the dimension of the inputs, which can easily be - at every time step;
-
the high computational cost required when integrating the model in time.
While uncertainty quantification is a very active field in general, its implementation and development for geosciences requires specific approaches that are investigated in Clime. The project-team tries to determine the best strategies for the generation of ensembles of simulations. In particular, this requires addressing the generation of large multimodel ensembles and the issue of dimension reduction and cost reduction. The dimension reduction consists in projecting the inputs and the state vector to low-dimensional subspaces. The cost reduction is carried out by emulation, i.e., the replacement of costly components with fast surrogates.
Application of sequential aggregation to meteorology
Participants : Paul Baudin, Vivien Mallet, Gilles Stoltz [CNRS] .
Nowadays, it is standard procedure to generate an ensemble of simulations for a meteorological forecast. Usually, meteorological centers produce a single forecast, out of the ensemble forecasts, computing the ensemble mean (where every model receives an equal weight). It is however possible to apply aggregation methods. When new observations are available, the meteorological centers also compute analyses. Therefore, we can apply the ensemble forecast of analyses, which consists in weighting the ensemble of forecasts to better forecast the forthcoming analyses. Before any forecast, the weights are updated with past observations and past forecasts. The performance of the aggregated forecast is guaranteed, in the long run, to perform at least as well as any linear combination of the forecasts with constant weights.
Ensembles of forecasts for mean sea level pressure, from the THORPEX Interactive Grand Global Ensemble, are aggregated with a forecast error decreased by 18% compared to the best individual forecast. The approach is also proved to be efficient for wind speed. The contribution of the ensembles (from different meteorological centers) to the performance increase are evaluated.
Sequential aggregation with uncertainty quantification and application to photovoltaics production
Participants : Paul Baudin, Vivien Mallet, Jean Thorey, Christophe Chaussin [EDF R&D] , Gilles Stoltz [CNRS] .
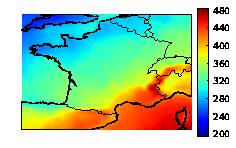
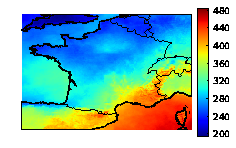
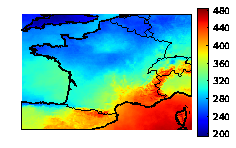
We study the aggregation of ensembles of solar radiations and photovoltaic productions. The aggregated forecasts show a 20% error decrease compared to the individual forecasts. They are also able to retrieve finer spatial patterns than the ones found in the individual forecasts (see Figure 5 ).
|
An important issue is the estimation of the uncertainties associated with the aggregated forecasts. We devise a new approach to predict a probability density function or a cumulative distribution function instead of a single aggregated forecast. In practice, the aggregation procedure aims at forecasting the cumulative distribution function of the observations which is simply a Heaviside function centered at the observed value. Our forecast is the weighted empirical cumulative distribution function based on the ensemble of forecasts. The method guarantees that, in the long run, the forecast cumulative distribution function has a Continuous Ranked Probability Score (CRPS) at least as good as the best weighted empirical cumulative function with weights constant in time.
The CRPS is a classical score to evaluate the probabilistic forecasts. However, applying the CRPS on weighted empirical distribution functions (derived from the weighted ensemble) introduces a bias because of which minimizing the CRPS does not produce the optimal weights. Thus, we propose an unbiased version of the CRPS which relies on clusters of members and is strictly proper.
Sensitivity analysis in the dispersion of radionuclides
Participants : Sylvain Girard, Vivien Mallet, Irène Korsakissok [IRSN] .
We carry out a sensitivity analysis of the dispersion of radionuclides during Fukushima disaster. We considered the dispersion at regional scale, with the Eulerian transport model Polair3D from Polyphemus. Simulations of the atmospheric dispersion of radionuclides involve large uncertainties originating from the limited knowledge of meteorological input data, composition, amount and timing of emissions and some model parameters. We studied the relative influence of each uncertain input on several outputs. In practice, we used the variance-based sensitivity analysis method of Sobol. This method requires a large number of model evaluations which are not achievable directly due to the high computational cost of the model. To circumvent this issue, we built a mathematical approximation of the model using Gaussian process emulation.
In previous studies, the uncertainties in the meteorological forecasts were crudely modeled by homogeneous and constant perturbations on the fields. Hence, we started investigating the use of ensembles of meteorological forecasts instead of just one base meterological forecast. Including such ensembles allows to better represent the directions along which meteorological uncertainties should lie.
Fire risk assessment
Participants : Jérémy Lefort, Vivien Mallet, Jean-Baptiste Filippi [CNRS] .
During days with extreme weather conditions, every wildland fire must be fought within minutes of its occurrence. This means that sufficient firefighting force is available at the right place and at the right time. In practice, firefighters wait at different critical locations, so that they can act quickly. For efficient preventive positioning of the firefighters, forecasting the risks of ignition of large fires is essential. This requires to predict where a fire may start, to estimate its potential size, to evaluate fighting scenarios and to anticipate which urban or protected areas may be under threat.
We designed a surrogate propagation model based on Gaussian process emulation of the model ForeFire. This surrogate model is fast enough to be run all over a region with high fire risk, e.g., Corsica. It can even be used for Monte Carlo simulations, with perturbations in the meteorological conditions and vegetation state, over Corsica. It is then possible to generate a risk map that identifies all the locations where a new fire can grow large.
Ensemble variational data assimilation
Participants : Julien Brajard, Isabelle Herlin, Marc Bocquet [CEREA] , Jérôme Sirven [LOCEAN] , Olivier Talagrand [LMD, ENS] , Sylvie Thiria [LOCEAN] .
The general objective of ensemble data assimilation is to produce an ensemble of analysis from observations and a numerical model which is representative of the uncertainty of the system. In a bayesian framework, the ensemble represents a sampling of the state vector probability distribution conditioned to the available knowledge of the system, denoted the a-posteriori probability distribution.
Ensemble variational data assimilation (EnsVar) consists in producing such an ensemble, by perturbating N times the observations according to their error law, and run a standard variationnal assimilation for each perturbation. An ensemble of N members is then produced. In the case of linear models, there is a theoretical guarantee that this ensemble is a sampling of the a-posteriori probability. But there is no theoretical result in the non-linear case.
Numerical experiments using non-linear numerical models suggest that the conclusion reached for linear models still stands for non-linear toy models.
The objective of this work is to study the ability of EnsVar to produce "good" ensemble (i.e. that sampled the a posteriori probablility) on a more realistic model: a shallow-water model. Some statistical properties of the ensemble are presented, and the sensitivity to the main features of the assimilation system (number, distribution of observations, size of the assimilation window, ...) are also studied.