Section: New Results

Programmable 2D Arrangements for Element Texture Design

Participants : Hugo Loi, Thomas Hurtut, Romain Vergne, Joëlle Thollot [contact] .

Figure 6. Element textures commonly used. These textures can be found in professional art (d,g,h), casual art (a,e,f), technical productions such as Computer-Assisted Design illustration tools (c), and textile industry (b). For each example, we show a hand-drawn image (left), and our synthesized reproduction of its geometric arrangement (right). (a,b,c) Classic regular distributions with contact, overlap and no adjacency between elements respectively. (d) Overlap of two textures creating cross hatching. (e) Non overlapping combination of two textures. (f,g,h) Complex element textures with clusters of elements. — Image credit: (d,g,h) “Rendering in Pen and Ink: The Classic Book On Pen and Ink Techniques for Artists, Illustrators, Architects, and Designers” ; (a,e) Profusion Art [profusionart.blogspot.com ]; (f) Hayes' Art Classes [hayesartclasses.blogspot.com ]; (c) CompugraphX [www.compugraphx.com ]; (b) 123Stitch [www.123stitch.com ].

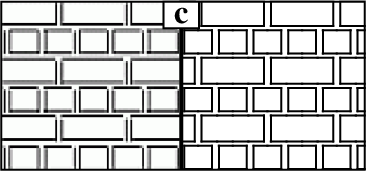
We introduce a programmable method for designing stationary 2D arrangements for element textures, namely textures made of small geometric elements. These textures are ubiquitous in numerous applications of computer-aided illustration. Previous methods, whether they be example-based or layout-based, lack control and can produce a limited range of possible arrangements. Our approach targets technical artists who will design an arrangement by writing a script. These scripts are using three types of operators: partitioning operators for defining the broad-scale organization of the arrangement, mapping operators for controlling the local organization of elements, and merging operators for mixing different arrangements. These operators are designed so as to guarantee a stationary result meaning that the produced arrangements will always be repetitive. We show (see Figure 10 ) that this simple set of operators is sufficient to reach a much broader variety of arrangements than previous methods. Editing the script leads to predictable changes in the synthesized arrangement, which allows an easy iterative design of complex structures. Finally, our operator set is extensible and can be adapted to application-dependent needs. This work is available as a research report [11]