Section: New Results
Piecewise polynomial Reconstruction of Scalar Fields from Simplified Morse-Smale Complexes
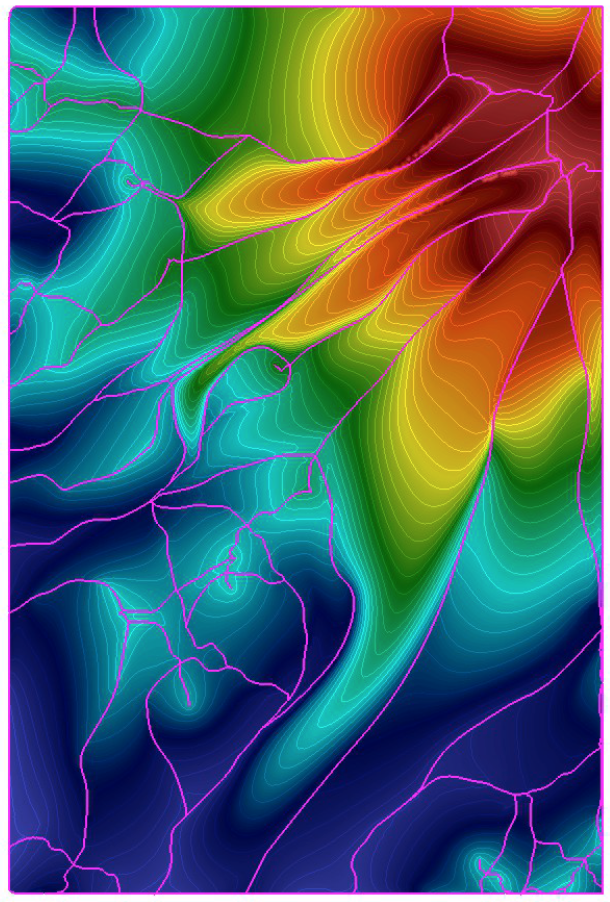
Participants : Léo Allemand-Giorgis, Georges-Pierre Bonneau [contact] .
|
Morse-Smale (MS) complexes have been proposed to visualize topological features of scalar fields defined on manifold domains. Herein, three main problems have been addressed in the past: (a) efficient computation of the initial combinatorial structure connecting the critical points; (b) simplification of these combinatorial structures; (c) reconstruction of a scalar field in accordance to the simplified Morse-Smale complex. The present paper faces the third problem by proposing a novel approach for computing a scalar field coherent with a given simplified MS complex that privileges the use of piecewise polynomial functions. Based on techniques borrowed from shape preserving design in Computer Aided Geometric Design, our method constructs the surface cell by cell using piecewise polynomial curves and surfaces. We present the benefit and limitations of using polynomials for reconstruction surfaces from topological data. This research was published in a book chapter [8] .