Section: New Results

High performance numerical computing

Porting a DGTD solver for bioelectromagnetics to the DEEP-ER architecture

Participants : Alejandro Duran [Barcelona Supercomputing Center, Spain] , Stéphane Lanteri, Raphaël Léger, Damian A. Mallón [Juelich Supercomputing Center, Germany] .

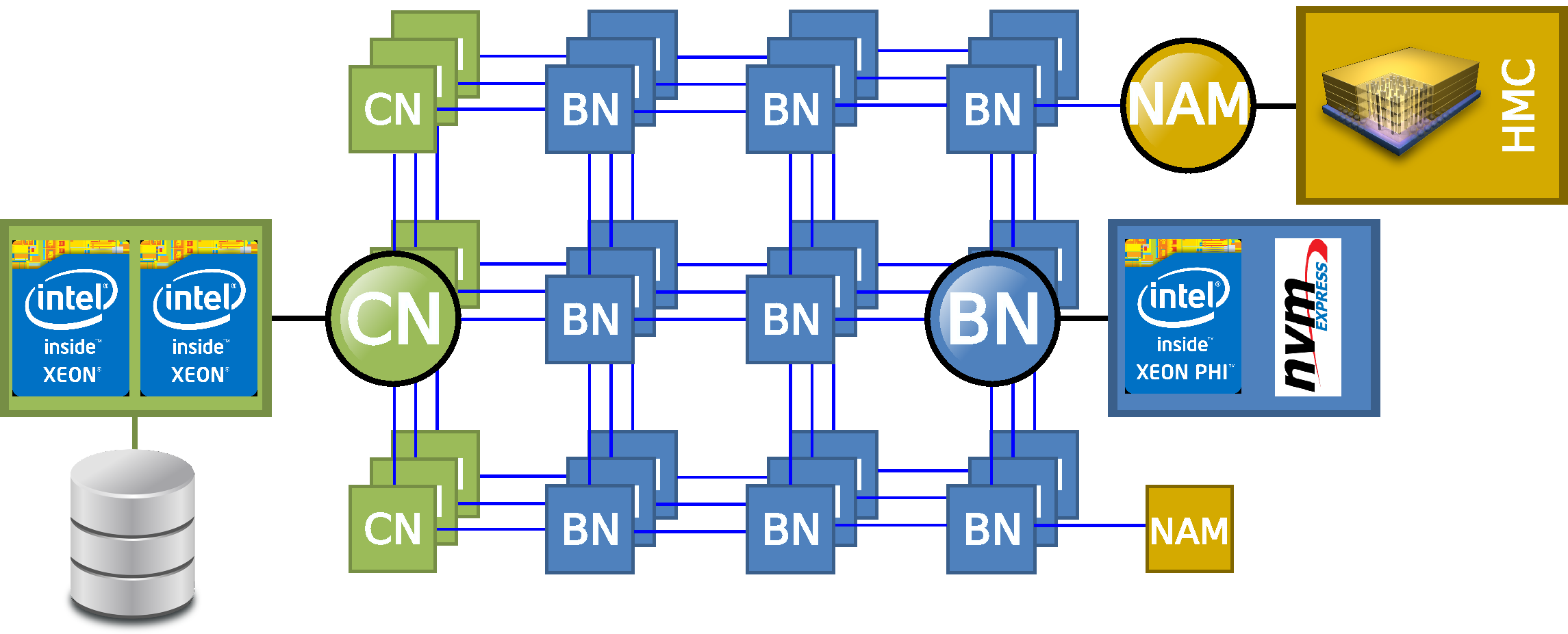
We are concerned here with the porting of a Discontinuous Galerkin Time-Domain solver for computational bioelectromagnetics to the novel heterogeneous architecture proposed in the DEEP-ER european project on exascale computing. This architecture is based on a Cluster/Booster division concept (see Fig. 6 ). The Booster nodes are based on the Intel Many Integrated Core (MIC) architecture. Therfore, one objective of our efforts is the algorithmic adaptation of the DG kernels in order to leverage the vectorizing capabilities of the MIC processor. The other activities that are undertaken in the context of our contribution to this project aim at exploiting the software environments and tools proposed by DEEP-ER partners for implementing resiliency strategies and high performance I/O operations. In particular, the Cluster nodes are used for running some parts of the pre- and post-processing phases of the DGTD solver which do not lend themselves well to multithreading, as well as I/O intensive routines. One possibility to achieve this is to consider a model in which these less scalable and I/O phases are reverse-offloaded from Booster processes to Cluster processes in a one-to-one mapping. This is achieved by exploiting the OmpSs offload functionality, developed at Barcelona Supercomputing Center for the DEEP-ER platform. In future work, the OmpSs framework will also be leveraged to expose task-based parallelism and exploit task-based resilience.

Hybrid MIMD/SIMD high order DGTD solver for nanophotonics

Participants : Tristan Cabel, Gabriel Hautreux [CINES, Montpellier] , Stéphane Lanteri, Raphaël Léger, Claire Scheid, Jonathan Viquerat.

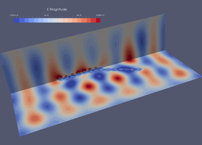
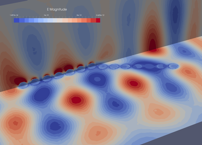
This work is concerned with the development of a scalable high order finite element type solver for the numerical modeling of light interaction with nanometer scale structures. From the mathematical modeling point of view, one has to deal with the differential system of Maxwell equations in the time domain, coupled to an appropriate differential model of the behavior of the underlying material (which can be a dielectric and/or a metal) at optical frequencies. For the numerical solution of the resulting system of differential equations, we adopt the high order DGTD (Discontinuous Galerkin Time-Domain) solver described in [21] . A hybrid MIMD/SIMD parallelization of this DGTD solver has been developed by combining the MPI and OpenMP parallel programming models. The performances of the resulting parallel DGTD solver have been assessed on the Curie system of the PRACE research infrastructure. For that purpose, we selected a use case typical of optical guiding applications. A Y-shaped waveguide is considered which consists in nanosphere embedded in vacuum (see Fig. 7 ). The constructed tetrahedral mesh consists of 520,704 vertices and 2,988,103 elements. The high order discontinuous finite element method designed for the solution of the system of time-domain Maxwell equations coupled to a Drude model for the dispersion of noble metals at optical frequencies is formulated on a tetrahedral mesh.