Section: New Results

Protocols and Models for Wireless Networks - Application to VANETs

Protocols for VANETs

An Infrastructure-Free Slot Assignment Algorithm for Reliable Broadcast of Periodic Messages in VANETs

Participants : Mohamed Elhadad, Paul Muhlethaler, Anis Laouiti.

We have designed a novel Distributed TDMA based MAC protocol, named DTMAC, developed specifically for a highway scenario. DTMAC is designed to provide the efficient delivery of both periodic and event-driven safety messages. The protocol uses the vehicles' location and a new slot reuse concept to ensure that vehicles in adjacent areas have a collision-free schedule. Simulation results and analysis in a highway scenario have been carried out to evaluate the performance of DTMAC and compare it with the VeMAC protocol.

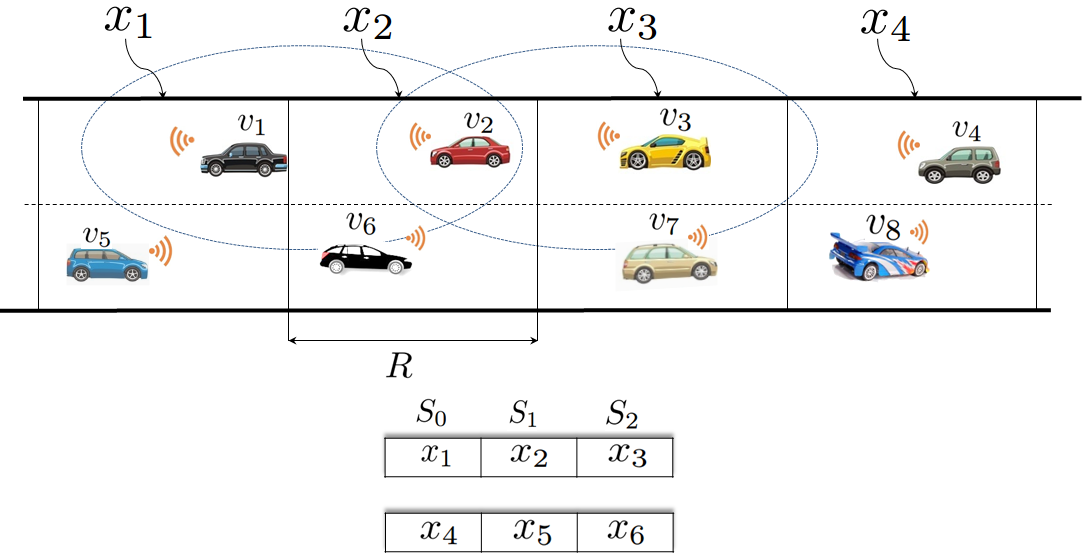
We propose a completely distributed and infrastructure free TDMA scheduling scheme which exploits the linear feature of VANET topologies. The vehicles' movements in a highway environment are linear due to the fact that their movements are constrained by the road topology. Our scheduling mechanism is also based on the assumption that each road is divided into $N$ small fixed areas, denoted by $x_i,i=1,...,N$ (see Figure 1). Area IDs can be easily derived using map and GPS Information.

The time slots in each TDMA frame are partitioned into three sets $S_0,S_1$ and $S_2$ associated with vehicles in three contiguous areas: $x_i,x_{i+1}$ and $x_{i+2}$, respectively (see Figure 1). Each frame consists of a constant number of time slots, denoted by $\tau$ and each time slot is of a fixed time duration, denoted by $s$. Each vehicle can detect the start time of each frame as well as the start time of a time slot. In the VANET studied, all the vehicles are equipped with a GPS and thus the one-Pulse-Per-Second (1PPS) signal that a GPS receiver gets from GPS satellites can be used for slot synchronization.

To prevent collisions on the transmission channel, our TDMA scheduling mechanism requires that every packet transmitted by any vehicle must contain additional information, called Frame Information (FI). For the frame, this field gives the status of the slot (Idle, Busy, Collision) and the ID of the vehicles accessing each slot with the characteristic of the data sent: periodic or event-driven safety messages.

The simulation results show that, compared to VeMAC which is the reference in terms of TDMA protocols for VANETs, DTMAC provides a lower rate of access and merging collisions, which results in significantly improved broadcast coverage. For further details see [27].

TRPM: a TDMA-aware routing protocol for multi-hop communications in VANETs

Participants : Mohamed Elhadad Or Hadded, Paul Muhlethaler, Anis Laouiti.

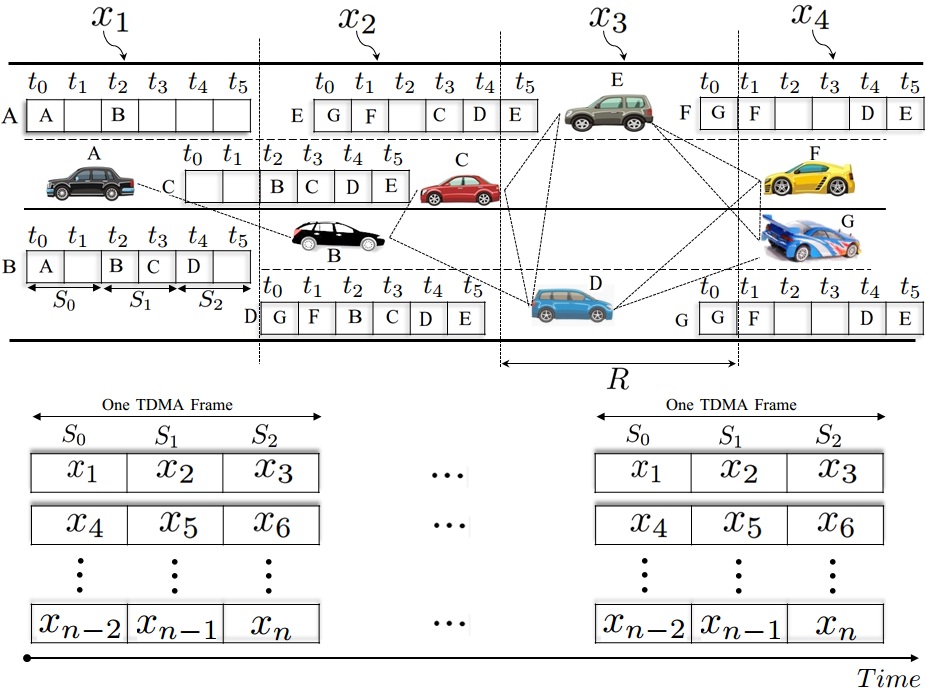
The main idea of TRPM is to select the next hop using the vehicle position and the time slot information from the TDMA scheduling. Like the GPSR protocol, we assume that each transmitting vehicle knows the position of the packet's destination. In TRPM, the TDMA scheduling information and the position of a packet's destination are sufficient to make correct forwarding decisions at each transmitting vehicle. Specifically, if a source vehicle is moving in area $x_i$, the locally optimal choice of next hop is the neighbor geographically located in area $x_{i+1}$ or $x_{i-1}$ according to the position of the packet's destination. As a result, the TDMA slot scheduling obtained by DTMAC can be used to determine the set of next hops that are geographically closer to the destination. In fact, each vehicle that is moving in the area $x_i$ can know the locally optimal set of next hops that are located in adjacent areas $x_{i+1}$ or $x_{i-1}$ by observing the set of time slots $S_{(i+3)\%3}$ or $S_{(i+1)\%3}$, respectively. We consider the same example presented above when vehicle G as the destination vehicle that will broadcast a message received from vehicle A. As shown in Figure 2, only two relay vehicles are needed to ensure a multi-hop path between vehicle A and G (one relay node in the area $x_2$ and another one in the area $x_3$).

In the following, the DTMAC protocol has been used by the vehicles to organize the channel access. The TDMA slot scheduling obtained by DTMAC is illustrated in Figure 2. Firstly, vehicle A forwards a packet to B, as vehicle A uses its frame information to choose a vehicle that is accessing the channel during the set $S_1$. Upon receiving the packet for forwarding, vehicle B will choose by using its frame information a vehicle that's accessing the channel during the set of time slots $S_2$ (say vehicle D). Then, vehicle D will forward the packet to G, as G is moving in area $x_4$ (accessing the channel during the set $S_0$) and it is the direct neighbor of vehicle D. By using DTMAC as the MAC layer, we can note that the path A-B-D-G is the shortest, in terms of the number of hops as well as the end-to-end delay which is equal to 6 time slots (2 time slots between $t_0$ and $t_2$ as $t_2$ is the transmission slot for vehicle B, then 2 time slots between $t_2$ and $t_4$ as $t_4$ is the transmission slot for vehicle D and finally 2 time slots between $t_4$ and $t_0$ as $t_0$ is the transmission slot in which vehicle G will broadcast the message received from vehicle A).

The idea of TRPM is the following. Whenever a vehicle $i$ accessing the channel during the set $S_k$ wants to send/forward an event-driven safety message, it constructs two sets of candidate forwarders based on its frame information FI as follows, where $TS\left(j\right)$ indicates the time slot reserved by vehicle $j$.

• $A_i=\{j\in N\left(i\right)|TS\left(j\right)\in S_{(k+1)\%3}\}$ // The set of vehicles that are moving in the adjacent right-hand area.

• $B_i=\{j\in N\left(i\right)|TS\left(j\right)\in S_{(k+2)\%3}\}$ // The set of vehicles that are moving in the adjacent left-hand area.

Each source vehicle uses the position of a packet's destination and the TDMA scheduling information to make packet forwarding decisions. In fact, when a source vehicle $i$ is moving behind the destination vehicle, it will select a next hop relay that belongs to set $B_i$; when the transmitter is moving in front of the destination vehicle, it will select a forwarder vehicle from those in set $A_i$. For each vehicle $i$ that will send or forward a message, we define the normalized weight function WHS (Weighted next-Hop Selection) which depends on the delay and the distance between each neighboring vehicle $j$. WHS is calculated as follows:

$WH{S}_{i,j}=\alpha *\frac{\Delta t_{i,j}}{\tau }-(1-\alpha )*\frac{d_{i,j}}{R}\left(1\right)$

Where:

• $\tau$ is the length of the TDMA frame (in number of time slots).

• $j$ is one of the neighbors of vehicle $i$, which represents the potential next hop that will relay the message received from vehicle $i$.

• $\Delta t_{i,j}$ is the gap between the sending slot of vehicle $i$ and the sending slot of vehicle $j$.

• $d_{i,j}$ is the distance between the two vehicles $i$ and $j$, and $R$ is the communication range.

• $\alpha$ is a weighted value in the interval $[0,1]$ that gives more weight to either distance or delay. When $\alpha$ is high, more weight is given to the delay. Otherwise, when $\alpha$ is small, more weight is given to the distance.

We note that the two weight factors $\frac{\Delta t_{i,j}}{\tau }$ and $\frac{d_{i,j}}{R}$ are in conflict. For simplicity, we assume that all the factors should be minimized. In fact, the multiplication of the second weight factor by (-1) allows us to transform a maximization to a minimization. Therefore, the forwarding vehicle for $i$ is the vehicle $j$ that is moving in an adjacent area for which $WH{S}_{i,j}$ is the lowest value.

The simulation results reveal that our routing protocol significantly outperforms other protocols in terms of average end-to-end delay, average number of relay vehicles and the average delivery ratio.

CTMAC: a Centralized TDMA for VANETs

Participants : Mohamed Elhadad Or Hadded, Paul Muhlethaler, Anis Laouiti.

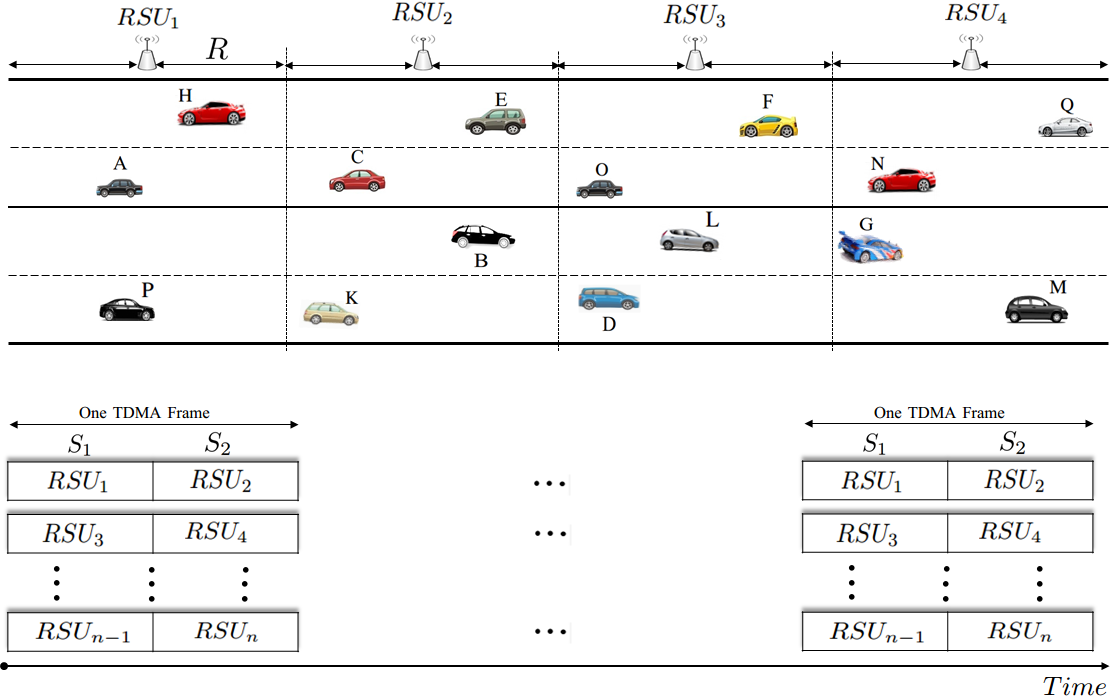
We have designed an infrastructure-based TDMA scheduling scheme which exploits the linear feature of VANET topologies. The vehicles' movements in a highway environment are linear due to the fact that their movements are constrained by the road topology. Our scheduling mechanism is also based on the assumption that the highway is equipped with some RSUs (i.e. one RSU for each $2\times Rmeters$, where $R$ is the communication range). Note that each area is covered by one RSU installed on the side of the highway and in the middle of the corresponding area. The time slots in each TDMA frame are partitioned into two sets $S_1,S_2$ associated with vehicles in two adjacent RSU areas (see Figure 3). Each frame consists of a constant number of time slots, denoted by $\tau$ and each time slot is of a fixed time duration, denoted by $s$. Each vehicle can detect the start time of each frame as well as the start time of a time slot.

The CTMAC scheduling mechanism uses a slot reuse concept to ensure that vehicles in adjacent areas covered by two RSUs have a collision-free schedule. The channel time is partitioned into frames and each frame is further partitioned into two sets of time slots $S_1$ and $S_2$. These sets are associated with vehicles moving in the adjacent RSU areas. These sets of time slots are reused along the highway in such a way that no vehicles belonging to the same set of two-hop neighbors using the same time slot. As shown in Figure 3, the vehicles in the coverage area of $RS{U}_1$ and those in the coverage area of $RS{U}_2$ are accessing disjoint sets of time slots. As a result, the scheduling mechanism of CTMAC can decrease the collision rate by avoiding the inter-RSUs interference without using any complex band. Each active vehicle keeps accessing the same time slot on all subsequent frames unless it enters another area covered by another RSU or a merging collision problem occurs. Each vehicle uses only its allocated time slot to transmit its packet on the control channel.

The simulation results reveal that CTMAC significantly outperforms the VeMAC and ADHOC MAC protocols. in terms of transmission collisions and the overhead required to create and maintain the TDMA schedules, see [28].

A Flooding-Based Location Service in VANETs

Participants : Selma Boumerdassi, Paul Muhlethaler.

This work was done in collaboration with Eric Renault, Telecom Sud Paris.

We have designed and analyzed a location service for VANETs; such a service can be used in Location-based routing protocols for VANETs. Our protocol is a proactive flooding-based location service that drastically reduces the number of update packets sent over the network as compared to traditional flooding-based location services. This goal is achieved by partially forwarding location information at each node. A mathematical model and some simulations are proposed to show the effectiveness of this solution. Cases for 1D, 2D and 3D spaces are studied for both deterministic and probabilistic forwarding decisions. We compare our protocol with the Multi-Point Relay (MPR) technique which is used in the OLSR protocol and determine the best technique according to the network conditions.

Models for Wireless Networks and VANETs

Performance analysis of IEEE 802.11 broadcast schemes with different inter-frame spacings

Participants : Younes Bouchaala, Paul Muhlethaler, Nadjib Achir.

This work has been in collaboration with Oyunchimeg Shagdar (Vedecom).

We have started to build a model which analyzes the performance of IEEE 802.11p managing different classes of priorities. The differentiation of traffic streams is obtained with different inter-frame spacings: AIFSs (for Arbitration Inter Frame Spacings) and with different back-off windows: CWs (for Collision Windows). This model is based on a Markov model where the state is the remaining number of idle slots that a packet of a given class has to wait before transmission. However, in addition to this Markov model for which we compute a steady state we also consider the Markov chain which counts the number of idle slots after the smallest AIFS. As a matter of fact the probability these states are not evenly distributed since with different AIFSs the arrival rate is not constant when the number of idle slots experienced after the smallest AIFS varies. The resolution of the steady state of these two inter-mixed Markov chains lead to non linear and intertwined equations that can be easily solved with a software such as Maple. With the model we have obtained, we can compute the delivery rate of packets of different classes and show the influence of system parameters: AIFSs and CWs. The preliminary results show a a very strong influence of different AIFSs on the performance for each traffic streams.

Model of IEEE 802.11 Broadcast Scheme with Infinite Queue

Participant : Paul Muhlethaler.

This work has been in collaboration with Guy Fayolle (Inria RITS).

We have analyzed the so-called back-off technique of the IEEE 802.11 protocol in broadcast mode with waiting queues. In contrast to existing models, packets arriving when a station (or node) is in back-off state are not discarded, but are stored in a buffer of infinite capacity. As in previous studies, the key point of our analysis hinges on the assumption that the time on the channel is viewed as a random succession of transmission slots (whose duration corresponds to the length of a packet) and mini-slots during which the back-off of the station is decremented. These events occur independently, with given probabilities. The state of a node is represented by a two-dimensional Markov chain in discrete-time, formed by the back-off counter and the number of packets at the station. Two models are proposed both of which are shown to cope reasonably well with the physical principles of the protocol. The stability (ergodicity) conditions are obtained and interpreted in terms of maximum throughput. Several approximations related to these models are also discussed. The results of this study are in [2].

Model and optimization of CSMA

Participants : Younes Bouchaala, Paul Muhlethaler, Nadjib Achir.

This work has been in collaboration with Oyunchimeg Shagdar (Vedecom).

We have studied the maximum throughput of CSMA in scenarios with spatial reuse. The nodes of our network form a Poisson Point Process (PPP) of a one- or two-dimensional space. The one-dimensional PPP well represents VANETs. To model the effect of Carrier Sense Multiple Access (CSMA), we give random marks to our nodes and to elect transmitting nodes in the PPP we choose the nodes with the smallest marks in their neighborhood, this is the Matern hardcore selection process. To describe the signal propagation, we use a signal with power-law decay and we add a random Rayleigh fading. To decide whether or not a transmission is successful, we adopt the Signal-over-Interference Ratio (SIR) model in which a packet is correctly received if its transmission power divided by the interference power is above a capture threshold. We assume that each node in our PPP has a random receiver at a typical distance. We choose the average distance to its closest neighbor. We also assume that all the network nodes always have a pending packet. With these assumptions, we analytically study the density of throughput of successful transmissions and we show that it can be optimized with the carrier-sense threshold. The model makes it possible to analytically compute the performance of a CSMA system and gives interesting results on the network performance such as the capture probability when the throughput is optimized, and the effect on a non-optimization of the carrier sense threshold on the throughput. We can also study the influence of the parameters and see their effects on the overall performance. We observe a significant difference between 2D an 1D networks.

We have built two models to compare the spatial density of successful transmissions of CSMA and Aloha. To carry out a fair comparison, we optimize both schemes by adjusting their parameters. For spatial Aloha, we can adapt the transmission probability, whereas for spatial CSMA we have to find the suitable carrier sense threshold. The results obtained show that CSMA, when optimized, outperforms Aloha for nearly all the parameters of the network model values and we evaluate the gain of CSMA over Aloha. We also find interesting results concerning the effect of the model parameters on the performance of both Aloha and CSMA. The closed formulas we have obtained provide immediate evaluation of performance, whereas simulations may take minutes to give their results. Even if Aloha and CSMA are not recent protocols, this comparison of spatial performance is new and provides interesting and useful results.

For Aloha networks, when we study transmissions over the average distance to the closest neighbor, the optimization does not depend on the density of nodes, which is a very interesting property. Thus in Aloha networks, the density of successful transmissions easily scales linearly in $\lambda$ when we vary $\lambda$ whereas in CSMA networks the protocol must be carefully tuned to obtain this scaling.

Adaptive CSMA

Participants : Nadjib Achir, Younes Bouchaala, Paul Muhlethaler.

This work has been in collaboration with Oyunchimeg Shagdar (Vedecom).

Using the model we have built for CSMA, we have shown that when optimized with the carrier sense detection threshold $P_{cs}$, the probability $p^{*}$ of transmission for a node in the CSMA network does not depend on the density of nodes $\lambda$. In other words when the CSMA is optimized to obtain the largest density of successful transmissions (communication from nodes to their neighbors), $p^{*}$ is constant. We have verified this statement on several examples and we think that a formal proof of this remark is possible using scaling arguments. The average access delay is a direct function of the probability of transmission $p$. Thus the average delay when the carrier sense detection threshold is optimized is a constant $D_{target}$ which does not depend on $\lambda$. A stabilization algorithm which adapts $P_{cs}$ to reach the $D_{target}$ can thus be envisioned.