Section: New Results

Robotics

Analysis of Cable-driven parallel robots

Participants : Alain Coulbois, Artem Melnyk, Jean-Pierre Merlet [correspondant] , Yves Papegay.

We have continued the analysis of suspended CDPRs for control and design purposes[12]. For control it is essential to determine the current pose of the robot for given cable lengths (forward kinematics, FK) and to be able to calculate the cable lengths for a given pose of the platform (inverse kinematics, IK). If the cables are supposed to be non-deformable the IK problem is trivial and has a single solution but the FK is complex, admits several solutions and raises several issues. We have shown in the past that to get all FK solutions for a CDPR with $m$ cables we have to consider not only the case where all cables are under tension but also have to solve the FK for all combinations of cables under tension with 1 to $m$ cables. Surprisingly the FK is more difficult if the CDPR has less than 6 cables under tension. Our team, in collaboration with M. Carricato of Bologna University, is the first to have designed a solving algorithm that allow to compute in a guaranteed manner all FK solutions while a theoretical approach has allowed us to provide a bound for the maximal number of solutions according to the number of cables under tension (respectively 24, 156, 216, 140 and 40 for 2, 3, 4, 5, 6 cables).

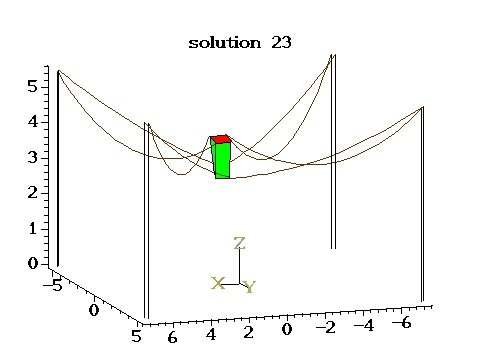
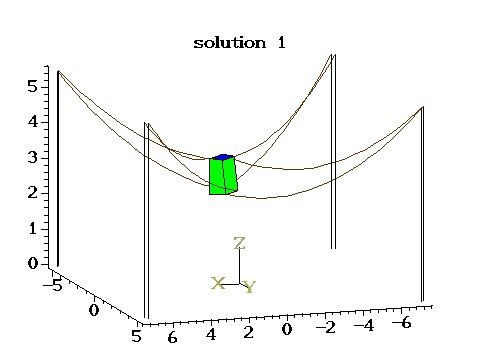
Even more complex kinematic problems are involved if we assume that the cable are catenary-like, which is valid for large dimension robot, and involves inverse hyperbolic functions and square root, prohibiting to use algebraic geometry tools for estimating the maximal number of solutions and for the solving. In that case both the IK and FK may have multiple solutions and we have exhibited last year interval analysis-based solving algorithms for the IK and FK based on our interval analysis library ALIAS , that is the only existing algorithm for managing such complex cables. However such algorithm has the drawback, beside being computer intensive, to provide only solution(s) within a given search space for the unknowns. In our IK and FK problems two unknowns for each cable are the horizontal and vertical components $F_x,F_z$ of the force exerted by the cables on the platform. In our case we have only the constraint $F_x>0$ and $F_z$ lower than half the mass of the cable but have no upper bound for $F_x$ and lower bound for $F_z$. We may choose arbitrary large values for these bounds at the expense of an exponentially increasing computation time. As for the IK, beside $F_x,F_z$, the length of the cable at rest $L_0$ is an unknown with $L_0>0$ but no known upper bound. This year we have both improved the interval analysis algorithms but have also explored an original continuation scheme that be used both for the IK and FK whatever is the cable model. The idea is to assume that the cable model includes a set of physical parameters $𝒫$ which describe the elastic and deformation behavior of the cable material. We assume that their are limit values ${𝒫}_r$ for these parameters such that the cable behave like a non-deformable, non-elastic cable while the real cable parameter is ${𝒫}_d$. For example for catenary cables elasticity is defined by the Young modulus $E$ of the cable material while the cable deformations is conditioned by its linear density $\mu$. If $E$ goes to infinity and $\mu$ to 0, then the cable is non-deformable, non-elastic. Now let us assume that we have a robot state for which the IK or FK are satisfied with the parameters $𝒫$. Assume that we modify ${𝒫}_d$ by a sufficient small amount $ϵ$ toward ${𝒫}_r$ so that the Newton scheme allow us to determine the new robot state for $𝒫={𝒫}_d+ϵ$. Proceeding iteratively along this way will lead us to a robot state that must be very close to one obtained for non deformable, non elastic cables. Now we may revert the process: starting from all the IK or FK solutions obtained for non deformable cables (corresponding to $𝒫={𝒫}_r$) we use Newton to compute a new robot state with $𝒫$ closer to ${𝒫}_d$ and doing that iteratively will lead to the solution(s) for $𝒫={𝒫}_d$). We have also shown that a safe value of $ϵ$ (ie. one that guarantee to obtain continuous solution without jump) may be calculated at each step by using the Kantorovitch theorem. We have implemented this principle for both the IK and FK problems (for 6 cables for the IK) and have found new IK and FK solutions which not been found previously because they were outside the search space of the interval analysis algorithms. A side benefit of this principle is that it has allowed us to be the first to provide an upper bound on the maximal number of solutions (63 for the IK of a robot with 6 cables, 33383 for the FK of a robot with 8 cables) whatever is the cable model. These new algorithms are much faster than the previous one (around one minute for the IK and 10 mn for the FK instead of several hours). However they raise a theoretical issue as the continuation scheme may lead to a solution that is close to be singular in which case the scheme cannot work. Understanding the singularity of the kinematics of CDPR is therefore a major problem. For the time being we mix the continuation scheme with the interval one that is basically used to solve the kinematic problem when the continuation scheme detect a singularity. As a test example we have considered a difficult CDPR with 8 cables and have shown a case with up to 41 solutions for the FK [10],[14],[11]. Figure 2 shows two of these solutions.

We have also investigated the calculation of cross-section of the workspace of CDPR [13]. We have shown that the border of this workspace for non deformable of purely elastic cables may be calculated rigorously by using an algorithm mixing a theoretical approach and numerical calculation. For catenary cables we have proposed a method that calculates a set of boxes that are guaranteed to lie in the workspace, getting smaller and smaller as soon as they are close to the border. Unfortunately this algorithm is highly computer intensive.

Cable-Driven Parallel Robots for additive manufacturing in architecture

Participant : Yves Papegay.

Easy to deploy and to reconfigure, dynamically efficient in large workspaces even with payloads, cable-driven parallel robots are very attractive for solving displacement and positioning problems in architectural building at scale 1 and seems to be a good alternative to crane and industrial manipulators in the area of additive manufacturing.

Based on the proof of concept developed during the previous collaboration with CNAM and Ecole Nationale Supérieure d'Architecture Paris-Malaquais, the design of a new large scale CDPR for additive manufacturing of building based on ultra-high performance concrete has started under our supervision.

A new partnership with the the XtreeE start-up company aiming at developing a real size industrial 3D-printer of concrete has been established.