Section: New Results

Aggregation Kinetics

Participants : Aurora Armiento, Tom Banks [CRSC, NCSU, Raleigh, USA] , Etienne Bernard, Thibault Bourgeron, José Antonio Carrillo [Imperial College, London, United Kingdom] , Marie Doumic, Dirk Drasdo, Miguel Escobedo [Universidad del País Vasco, Bilbao, Spain] , Sarah Eugène, Pierre Gabriel [Université Paris-Dauphine] , Marc Hoffmann [Ceremade, Université Paris-Dauphine] , François James [MAPMO, Université d'Orléans] , Nathalie Krell [Université de Rennes 1] , Frédéric Lagoutière [Département de mathématiques d'Orsay] , Philippe Moireau [Inria Paris Saclay, M3DISIM project-team] , Benoît Perthame, Stéphanie Prigent, Human Rezaei [VIM, INRA Jouy-en-Josas] , Lydia Robert [Laboratoire Jean Perrin, UPMC] , Philippe Robert [Inria Paris, RAP project-team] , Maria Teresa Teixeira [IBCP, Paris] , Joan Torrent [INRA, Jouy-en-josas] , Magali Tournus [Ecole Centrale de Marseille] , Nicolas Vauchelet, Min Tang [Jiaotong University, Shanghai] , Zhou Xu [IBCP, Paris] , Wei-Feng Xue [University of Kent, United Kingdom] , Yi Yin.

Heterogeneity as an intrinsic feature in biological dynamics

Variability in nucleated polymerisation The kinetics of amyloid assembly show an exponential growth phase preceded by a lag phase, variable in duration as seen in bulk experiments and experiments that mimic the small volumes of cells. Sarah Eugène's Ph.D, defended in September 2016, was devoted to the study of the origins and the properties of the observed variability in the lag phase of amyloid assembly currently not accounted for by deterministic nucleation dependent mechanisms. In [20], we formulated a new stochastic minimal model that is capable of describing the characteristics of amyloid growth curves despite its simplicity. We then solve the stochastic differential equations of our model and give mathematical proof of a central limit theorem for the sample growth trajectories of the nucleated aggregation process. These results give an asymptotic description for our simple model, from which closed form analytical results capable of describing and predicting the variability of nucleated amyloid assembly were derived. We also demonstrate the application of our results to inform experiments in a conceptually friendly and clear fashion. Our model offers a new perspective and paves the way for a new and efficient approach on extracting vital information regarding the key initial events of amyloid formation.

However, this first model does not explain completely the variability observed in the experiments. In [17], we thus investigated extensions to take into account other mechanisms of the polymerisation process that may have an impact on fluctuations.The first variant consists in introducing a preliminary conformation step to take into account the biological fact that, before being polymerised, a monomer has two states, regular or misfolded. Only misfolded monomers can be polymerised so that the fluctuations of the number of misfolded monomers can be also a source of variability of the number of polymerised monomers. The second variant represents the reaction rate of spontaneous formation of a polymer as of the order of $\alpha$, with $\alpha$ some positive constant. First and second order results for the starting instant of nucleation are derived from these limit theorems. The proofs of the results rely on a study of a stochastic averaging principle for a model related to an Ehrenfest urn model, and also on a scaling analysis of a population model.

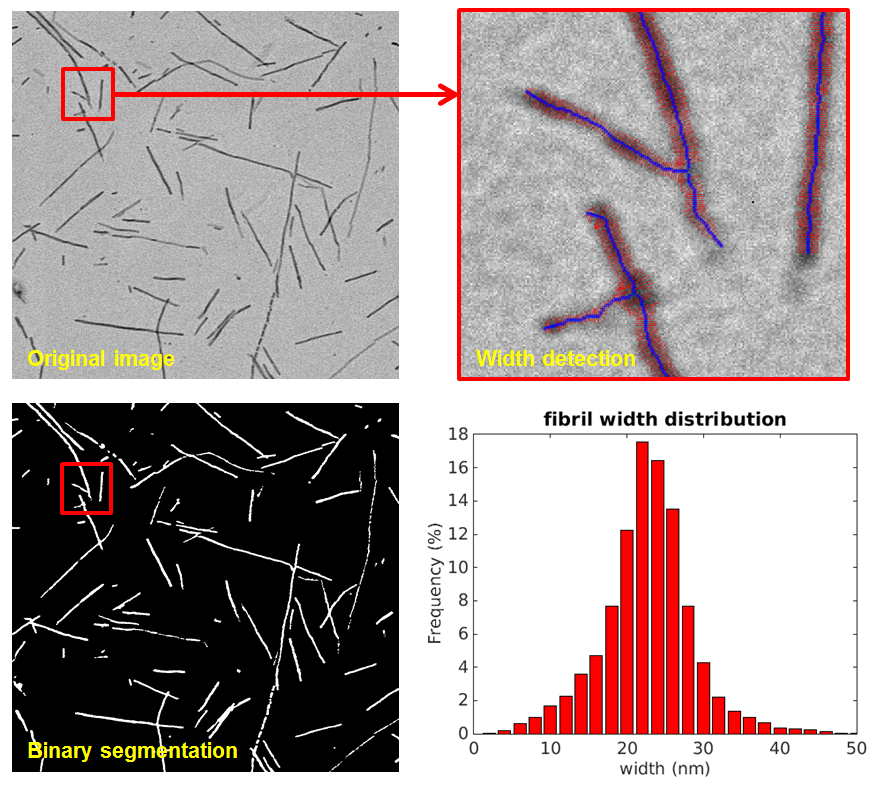
Image and statistical analysis of protein fibrils Protein fibrils present an important structural diversity, not only their length, but also their width, whether they present branches or not, etc. These structures may reveal the presence of different types of aggregates, possibly formed out of different polymerisation pathways. To analyse this diversity of shapes and structures, we developed an image analysis software, based on the expertise acquired by Y. Yin during her PhD for the image analysis of vessels. This software is able to track fibrils and measure their length, number of branches, and variable widths, even with poor quality images and crossing fibrils. This done, it allows us to perform a statistical analysis of the fibrils, to elucidate the main structuring features (Figure 3).

Inverse Problems and Data Assimilation Applied to Protein Aggregation and other settings

Estimating reaction rates and size distributions of protein polymers is an important step for understanding the mechanisms of protein misfolding and aggregation, a key feature for amyloid diseases. A. Armiento's Ph.D was devoted to the question of adapting data assimilation strategies to the specific context and difficulties of protein aggregation. In [6], we settled a framework problem when the experimental measurements consist in the time-dynamics of a moment of the population (i.e., for instance the total polymerised mass, as in Thioflavine T measurements, or the second moment measured by Static Light Scattering). We propose a general methodology, and we solve the problem theoretically and numerically in the case of a depolymerising system. We then apply our method to experimental data of degrading oligomers, and conclude that smaller aggregates of ovPrP protein should be more stable than larger ones. This has an important biological implication, since it is commonly admitted that small oligomers constitute the most cytotoxic species during prion misfolding process.

Time asymptotics for growth-fragmentation equations

The long-term dynamics of fragmentation and growth-fragmentation equations has constantly been for the MAMBA (and for the ex-BANG) team an important research field. Thanks to these common efforts, these equations are now well understood. However, there remain some interesting open questions. In particular, if the generic long-time behaviour for the linear equation is known - given by a (generally exponential) trend towards a steady exponential growth described by the positive eigenvector linked to the dominant eigenvalue, see  [83] for most recent results - critical cases are not yet fully understood.

With Miguel Escobedo, we focused on an important critical case, when the fragmentation is constant and the growth rate is either null or linear [16]. Using the Mellin transform of the equation, we determine the long time behaviour of the solutions and the speed of convergence, which may be either exponential or at most polynomial according to the subdomain of $(t,x)\in {\mathrm{I}\mathrm{R}}_{+}^2$ which is considered. Our results show in particular the strong dependence of this asymptotic behaviour with respect to the initial data, in contrast to the generic results. Following our study, J. Bertoin and A. Watson proposed a complementary probabilistic analysis of related models  [57]. These results exemplify the continuing need for further analysis of these interesting equations.

With E. Bernard and P. Gabriel, in [36], we investigated the “idealised” mitotic case, when the growth is exponential and the division results in two exactly equal parts. This case exhibits a lack of dissipativity, and the solutions appear to have a periodic limit cycle. We were nonetheless able to prove an entropy inequality, and to express the limit as an explicit oscillatory function, analytically given by the projection of the initial state on the space generated by the countable set of the dominant eigenvectors of the operator.

Cell aggregation by chemotaxis

Bacterial chemotaxis is now a well-known phenomenon. In particular, it has been established that the motion of bacteria is due to the alternation of straight swims in a given direction with tumble phases. More precisely, when bacteria notice that they do not go in a favorable direction, they may change their direction. Well established models are now available. In particular, the use of such systems allows to recover successfully the behaviour observed in biological experiments (see e.g. [18]). The bacterial response to changes in their environment can be described by an internal variable. In a recent work [29], it has been established that a well-known kinetic model can be obtained from such a model incorporating an internal variable.

When, the frequency of tumbling is high, the motion is mainly driven by tumbling and models reduce to describe aggregation phenomena. From a mathematical point of view, the study of such model is challenging since classical solution may not exist for any time. Then a notion of weak measure solution should be introduced [10]. Numerical investigation of such solutions has been performed in [21], [48].