Section: New Results

Visualization and Geometric Design

Surfacing Curve Networks with Normal Control

Participant : Georges-Pierre Bonneau.

Members of Maverick involved: Georges-Pierre Bonneau

This is a joint work with team-project IMAGINE (Tibor Stanko and Stefanie Hahmann) at Inria-Grenoble and CEA-Leti (Nathalie Saguin). Recent surface acquisition technologies based on microsensors produce three-space tangential curve data which can be transformed into a network of space curves with surface normals. This work addresses the problem of surfacing an arbitrary closed 3D curve network with given surface normals. Thanks to the normal vector input, the patch finding problem can be solved unambiguously and an initial piecewise smooth triangle mesh is computed. The input normals are propagated throughout the mesh. Together with the initial mesh, the propagated normals are used to compute mean curvature vectors. We compute the final mesh as the solution of a new variational optimization method based on the mean curvature vectors. The intuition behind this original approach is to guide the standard Laplacian-based variational methods by the curvature information extracted from the input normals. The normal input increases shape fidelity and allows to achieve globally smooth and visually pleasing shapes [2], [7]. This is a joint work with team-project IMAGINE (Tibor Stanko and Stefanie Hahmann) at Inria-Grenoble and CEA-Leti (Nathalie Saguin).

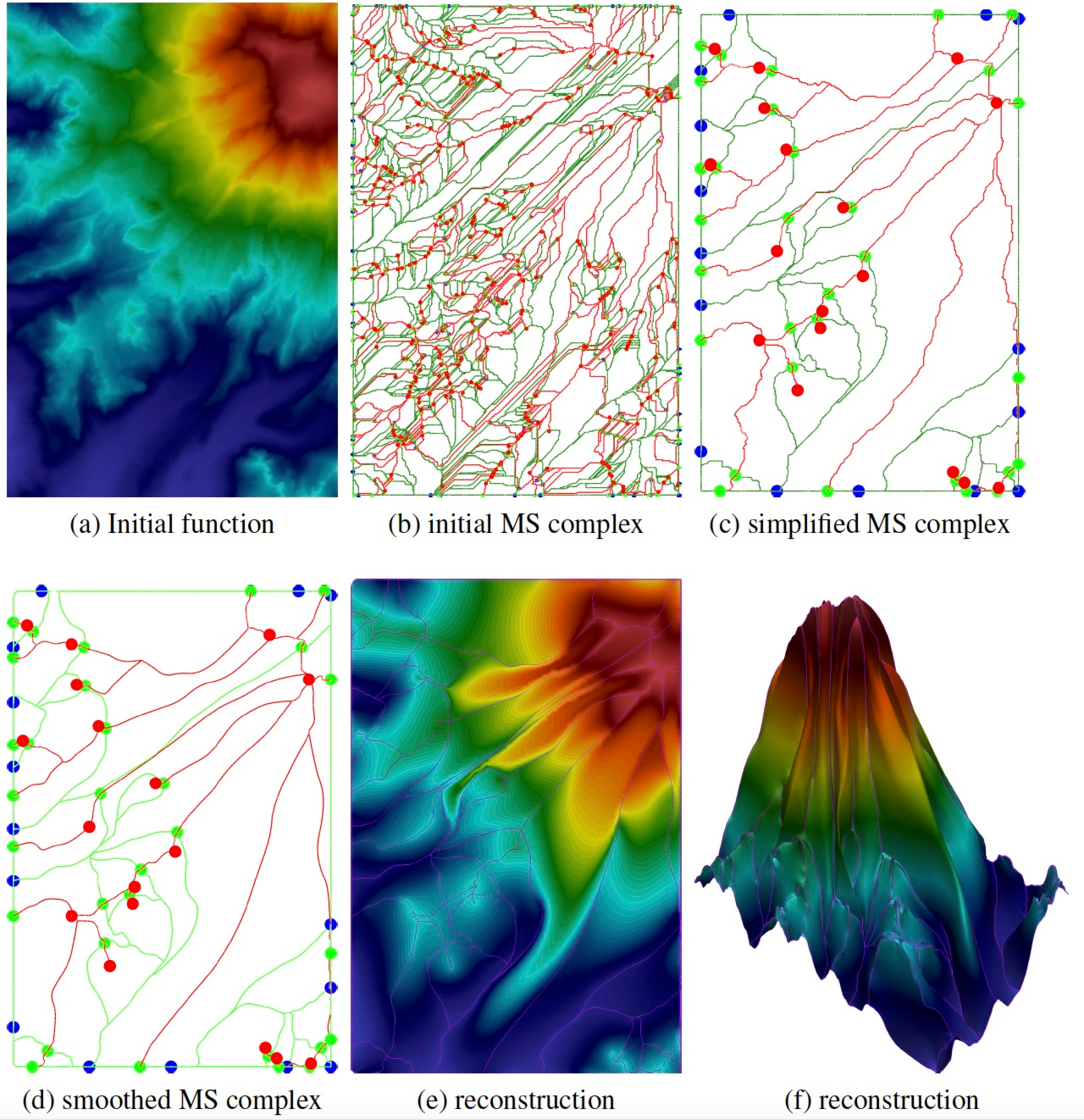
Piecewise polynomial Reconstruction of Scalar Fields from Simplified Morse-Smale Complexes

Participants : Léo Allemand-Giorgis, Georges-Pierre Bonneau.

Morse-Smale (MS) complexes have been proposed to visualize topological features of scalar fields defined on manifold domains. Herein, three main problems have been addressed in the past: (a) efficient computation of the initial combinatorial structure connecting the critical points; (b) simplification of these combinatorial structures; (c) reconstruction of a scalar field in accordance to the simplified Morse-Smale complex. The present work faces the third problem by proposing a novel approach for computing a scalar field coherent with a given simplified MS complex that privileges the use of piecewise polynomial functions. Based on techniques borrowed from shape preserving design in Computer Aided Geometric Design, our method constructs the surface cell by cell using piecewise polynomial curves and surfaces. The benefit and limitations of using polynomials for reconstruction surfaces from topological data are studied in this work [14].