Section: New Results
Advanced Numerical Modeling and Simulation
Face-based Smoothed Finite Element Method for Real-time Simulation of Soft Tissue
Participants: A. Mendizabal, C. Paulus, R. Bessard-Duparc, I. Peterlik, S. Cotin
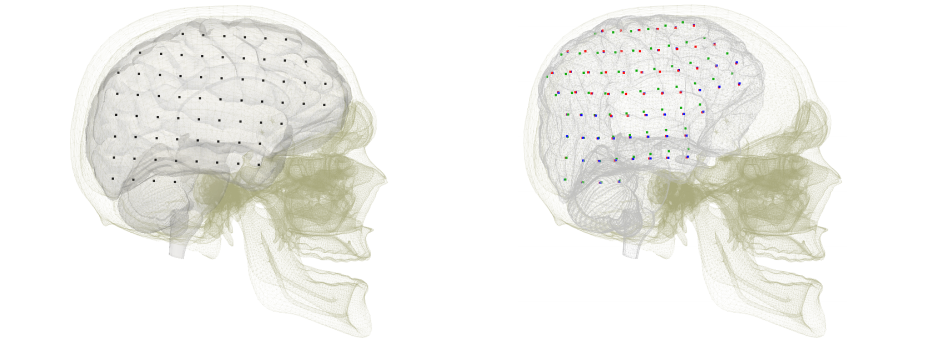
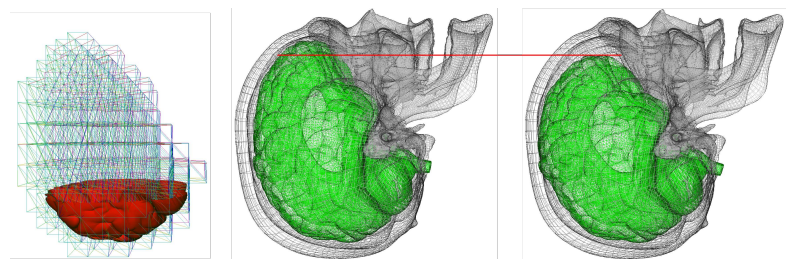
A method based on face-based smoothed finite element method was proposed and applied in the context of modeling of brain shift in [23]. This numerical technique has been introduced recently to overcome the overly stiff behavior of the standard FEM and to improve the solution accuracy and the convergence rate in solid mechanics problems. In this paper, a face-based smoothed finite element method (FS-FEM) using 4-node tetrahedral elements is presented. We show that in some cases, the method allows for reducing the number of degrees of freedom, while preserving the accuracy of the discretization. The method is evaluated on a simulation of a cantilever beam loaded at the free end and on a simulation of a 3D cube under traction and compression forces. Further, it is applied to the simulation of the brain shift and of the kidney's deformation. The results demonstrate that the method outperforms the standard FEM in a bending scenario and that has similar accuracy as the standard FEM in the simulations of brain shift and kidney deformation.
|
Immersed Boundary Method for Real-time
Participants: C. Paulus, S. Cotin
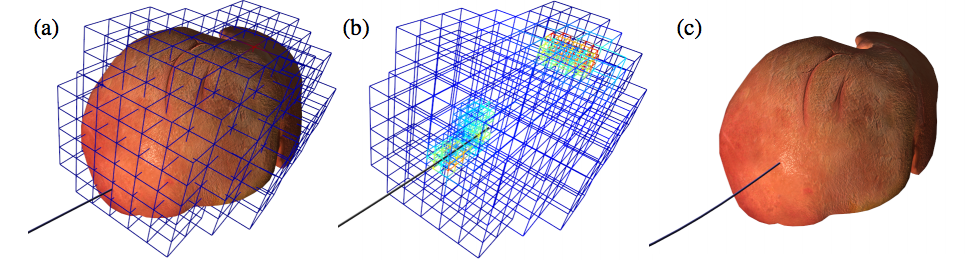
Although the finite element method is widely used as a numerical approach in this area, it is often hindered by the need for an optimal meshing of the domain of interest. The derivation of meshes from imaging modalities such as CT or MRI can be cumbersome and time-consuming. In our contribution [24], we employed the Immersed Boundary Method (IBM) to bridge the gap between these imaging modalities and the fast simulation of soft tissue deformation on complex shapes represented by a surface mesh directly retrieved from binary images. A high resolution surface, that can be obtained from binary images using a marching cubes approach, is embedded into a hexahedral simulation grid. The details of the surface mesh are properly taken into account in the hexahedral mesh by adapting the Mirtich integration method. In addition to not requiring a dedicated meshing approach, our method results in higher accuracy for less degrees of freedom when compared to other element types. Examples on brain deformation demonstrate the potential of our method.
|
Error Control in Surgical Simulations
Participants: H. Courtecuisse, S. Cotin
A contribution [16] presents the first real-time a posteriori error-driven adaptive finite element approach for real-time simulation and demonstrates the method on a needle insertion problem.
We use corotational elasticity and a frictional needle–tissue interaction model. The problem is solved using finite elements and the refinement strategy relies upon a hexahedron-based finite element method, combined with a posteriori error estimation driven local h-refinement, for simulating soft tissue deformation. We proposed to control the local and global error level in the mechanical fields (e.g. displacement or stresses) during the simulation. We show the convergence of the algorithm on academic examples, and demonstrate its practical usability on a percutaneous procedure involving needle insertion in a liver. For the latter case, we compare the force displacement curves obtained from the proposed adaptive algorithm with that obtained from a uniform refinement approach. Error control guarantees that a tolerable error level is not exceeded during the simulations. Local mesh refinement accelerates simulations. The work provides a first step to discriminate between discretization error and modeling error by providing a robust quantification of discretization error during simulations.