Section: New Results

Approximation

Variance-Minimizing Transport Plans for Inter-surface Mapping

Participants : Pierre Alliez, Mathieu Desbrun.

In collaboration with Manish Mandad (former Ph.D. student) and Prof. Leif Kobbelt from RWTH Aachen, and with David Cohen-Steiner from the DataShape project-team.

We contribute an efficient computational method for generating dense and low distortion maps between two arbitrary surfaces of same genus [19]. Instead of relying on semantic correspondences or surface parameterization, we directly optimize a variance-minimizing transport plan between two input surfaces that defines an as-conformal-as-possible inter-surface map satisfying a user-prescribed bound on area distortion. The transport plan is computed via two alternating convex optimizations, and is shown to minimize a generalized Dirichlet energy of both the map and its inverse. Computational efficiency is achieved through a coarse-to-fine approach in diffusion geometry, with Sinkhorn iterations modified to enforce bounded area distortion. The resulting inter-surface mapping algorithm applies to arbitrary shapes robustly (figure 10), with little to no user interaction. This work has been published at the ACM SIGGRAPH conference.

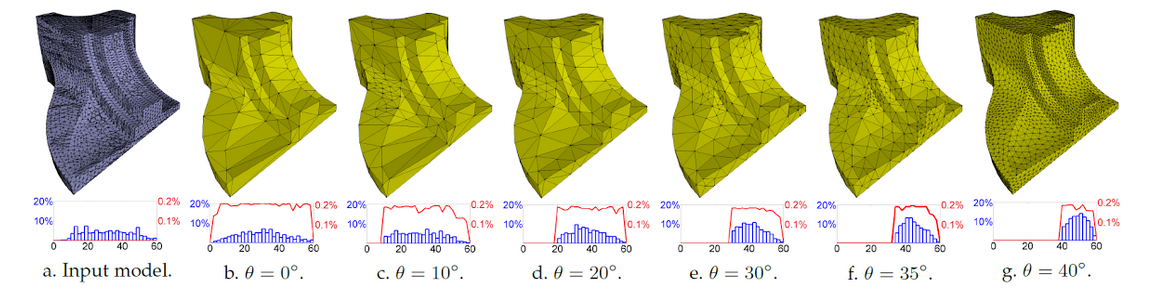
Error-Bounded and Feature Preserving Surface Remeshing with Minimal Angle Improvement

Participant : Pierre Alliez.

In collaboration with Kaimo Hu (former post-doc) and Bedrich Benes from Purdue University, with David Bommes from RWTH Aachen and Dong-Ming Yan from the National Laboratory of Pattern Recognition, Institute of Automation, Chinese Academy of Sciences.

Surface remeshing is a key component in many geometry processing applications. The typical goal consists in finding a mesh that is (1) geometrically faithful to the original geometry, (2) as coarse as possible to obtain a low-complexity representation and (3) free of bad elements that would hamper the desired application. Our remeshing algorithm [15] is designed to address all three optimization goals simultaneously by targeting prescribed bounds on approximation error, minimal interior angle and maximum mesh complexity. Our optimization framework applies carefully prioritized local operators in order to greedily search for the coarsest mesh with minimal interior angle and bounded approximation error. Fast runtime is enabled by a local approximation error estimation, while implicit feature preservation is obtained by specifically designed vertex relocation operators. Experiments show that our approach delivers high-quality meshes with implicitly preserved features and better balances between geometric fidelity, mesh complexity and element quality than the state-of-the-art (Figure 11). This work has been published in the IEEE Transactions on Visualization and Computer Graphics, and was presented at the EUROGRAPHICS Symposium on Geometry Processing.