Section: New Results

Hex-dominant meshing: Mind the gap!

Participants : Nicolas Ray, Dmitry Sokolov, Maxence Reberol, Franck Ledoux, Bruno Lévy.

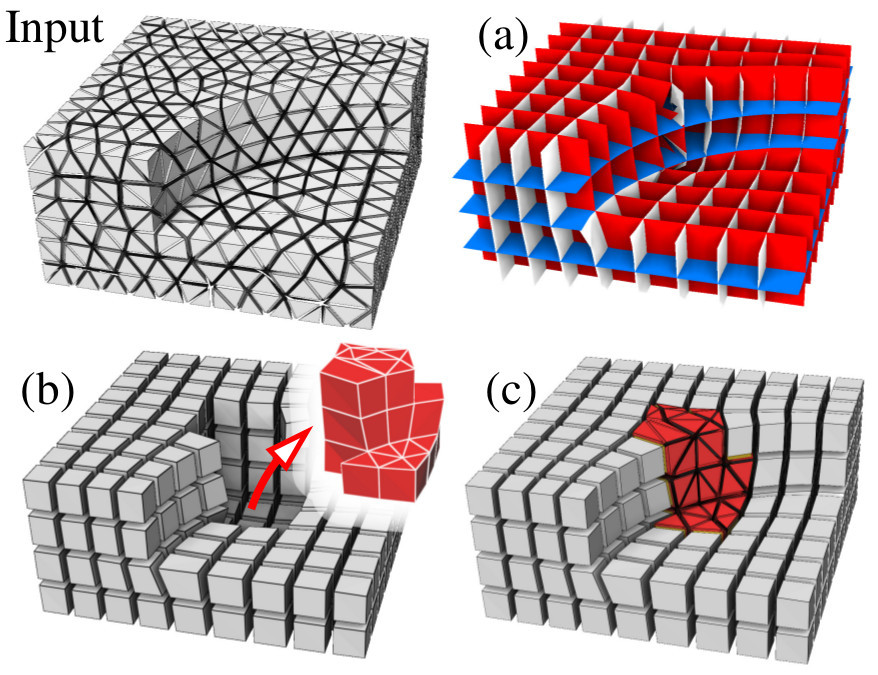
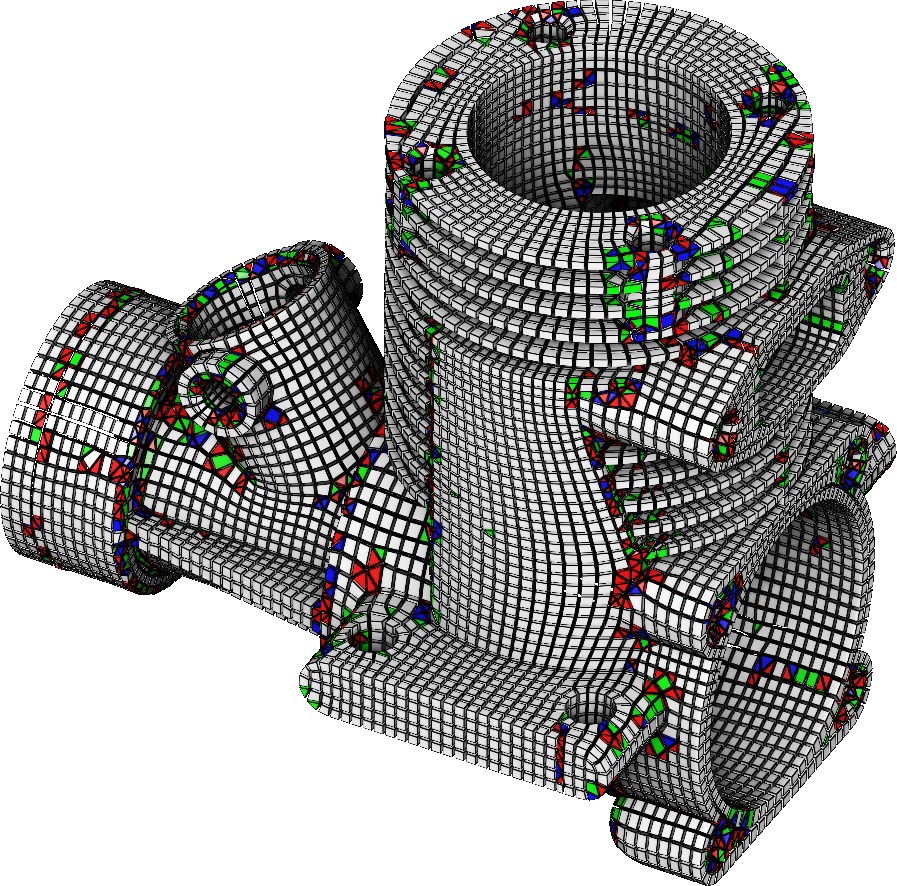
We proposed a robust pipeline that can generate hex-dominant meshes from any global parameterization of a tetrahedral mesh (Figure 1). We focus on robustness in order to be able to benchmark different parameterizations on a large database. Our main contribution is a new method that integrates the hexahedra (extracted from the parameterization) into the original object. The main difficulty is to produce the boundary of the result, composed of both faces of hexahedra and tetrahedra. Obviously, this surface must be a good approximation of the original object but, more importantly, it must be possible to remesh the volume bounded by this surface minus the extracted hexahedra (called void). We enforce these properties by carefully tracking and eliminating all possibilities of failure at each step of our pipeline.

We tested our method on a large collection of objects (200+) with different settings. In most cases, we obtained results of very good quality as compared to the state-of-the-art solutions.

Figure 1. Our hexahedral-dominant meshing procedure: Start from an input tetrahedral mesh. Compute a global parameterization (a). Extract hexahedra by contouring the isovalues of the parameterization. Isolate the boundary of the void (in red), i.e., the volume with a degenerate / singular parameterization (b) (also called “gap” or “cavity”), shown in red. Remesh the void and stitch it into the hexahedral mesh (c).