Section: New Results
Meshless Voronoi on the GPU
Participants : Nicolas Ray, Dmitry Sokolov, Sylvain Lefebvre, Bruno Lévy.
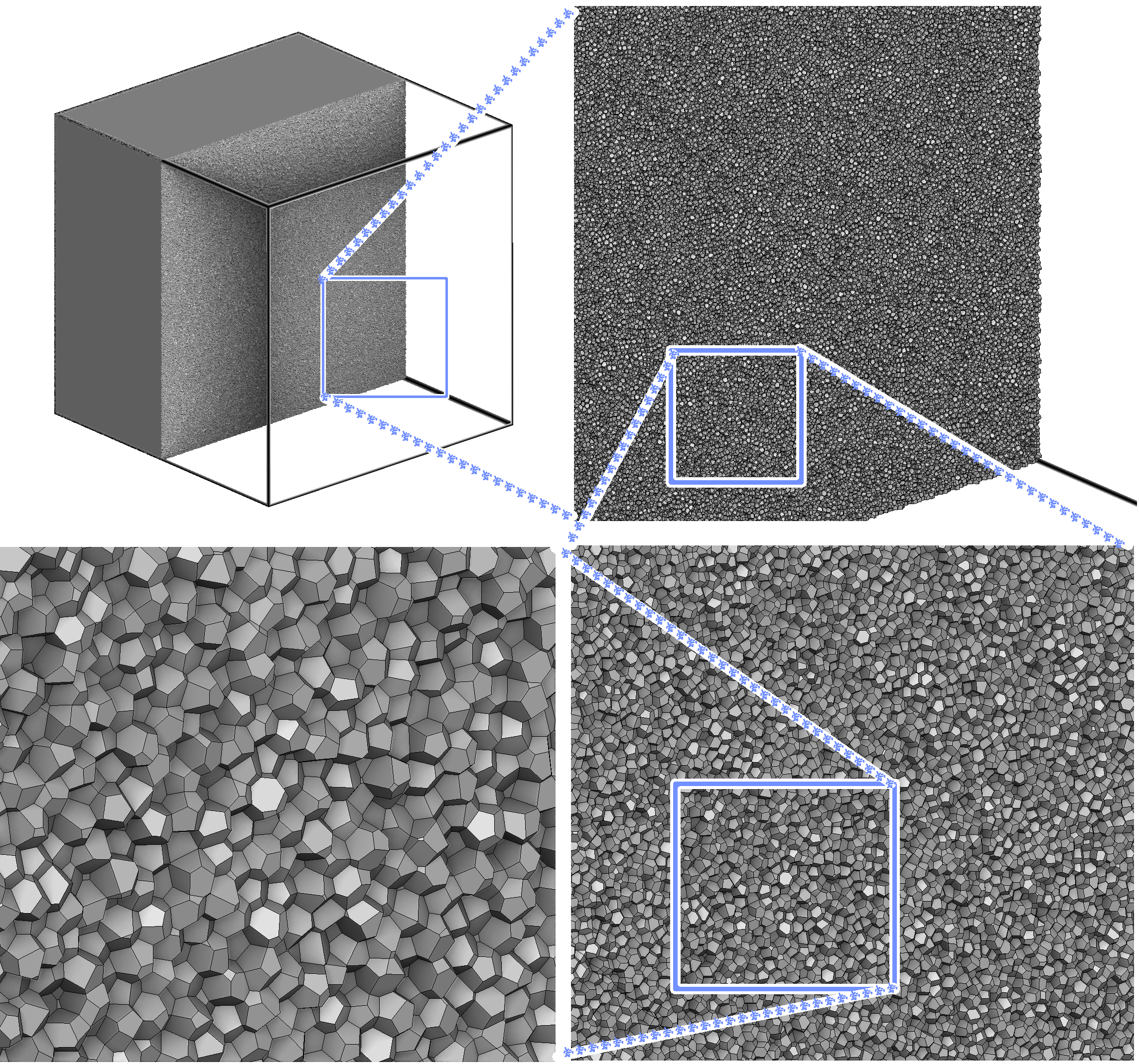
We proposed a GPU algorithm that computes a 3D Voronoi diagram (Figure 2). Our algorithm is tailored for applications that solely make use of the geometry of the Voronoi cells, such as Lloyd's relaxation used in meshing, or some numerical schemes used in fluid simulations and astrophysics. Since these applications only require the geometry of the Voronoi cells, they do not need the combinatorial mesh data structure computed by the classical algorithms (Bowyer-Watson). Thus, by exploiting the specific spatial distribution of the point-sets used in this type of applications, our algorithm computes each cell independently, in parallel, based on its nearest neighbors. In addition, we show how to compute integrals over the Voronoi cells by decomposing them on the fly into tetrahedra, without needing to compute any combinatorial information. The advantages of our algorithm is that it is fast, very simple to implement, has constant memory usage per thread and does not need any synchronization primitive. These specificities make it particularly efficient on the GPU: it gains one order of magnitude as compared to the fastest state-of-the-art multicore CPU implementations. To ease the reproducibility of our results, the full documented source code is included in the supplemental material.