Section: New Results

All-speed multi-material schemes

We are interested in the development of numerical models for phenomena involving fluid flows and elastic material deformations. We pursue a monolithic approach, which describes the behavior of each material (gas, liquid or solid) through a system of conservation laws and appropriate constitutive relationships. Our method is designed to handle both high-Mach and low-Mach regimes.

It is well-known that Godunov-type schemes are inadequate for low-Mach problems: first, they introduce an eccessive amount of numerical artificial viscosity; second, they require the enforcement of a CFL stability condition which leads to unpractical time steps. For this reason, we resort to the relaxation method proposed in [36], to derive a novel discretization scheme which can be applied to problems characterized by a broad range of Mach numbers. As opposed to [36], we propose in [1] to treat the advective term implicitly.

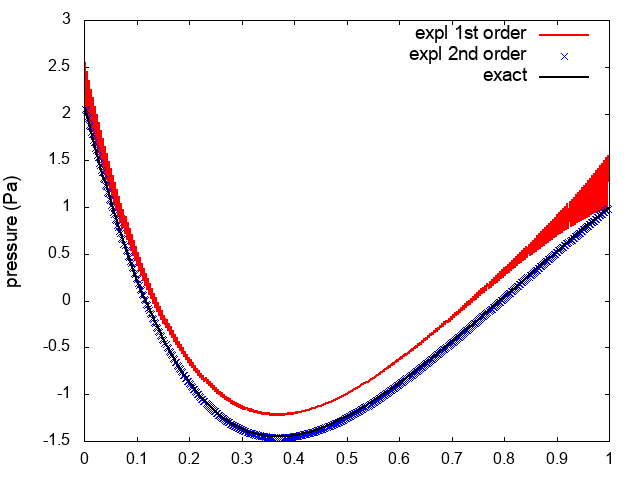
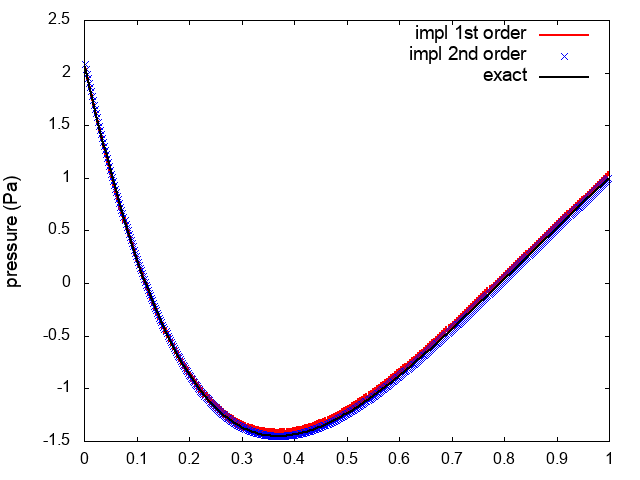
Figure 7 shows results for a quasi 1D de Laval nozzle problem in water: the flow is low-Mach and almost incompressible. In the present simulation, we impose at the inlet the total pressure $P_{\mathrm{tot}}=10\mathrm{Pa}$ and the absolute temperature $T=280K$ and at the outlet the pressure $p_{\mathrm{out}}=1\mathrm{Pa}$. Figure 7(center) shows results for the explicit scheme proposed in [36], while Figure 7(right) shows results of our implicit scheme; for the explicit schemes, we impose the acoustic CFL ${\nu }_{\mathrm{ac}}=0.4$, while for the implicit scheme, we consider ${\nu }_{\mathrm{ac}}=100$. We observe that our method outperforms the method in [36].

Figure 7. all-speed relaxation scheme. Left: de Laval nozzle. Center: pressure distribution predicted by the explicit method in [36] (${\nu }_{\mathrm{ac}}=0.4$). Right: pressure distribution predicted by the implicit method proposed in [1] (${\nu }_{\mathrm{ac}}=100$).