Section: New Results

Domain decomposition methods

Transparent boundary conditions with overlap in unbounded anisotropic media

Participants : Anne-Sophie Bonnet Ben-Dhia, Sonia Fliss, Yohanes Tjandrawidjaja.

This work is done in the framework of the PhD of Yohanes Tjandrawidjaja (funded by CEA-LIST), in collaboration with Vahan Baronian (CEA). This follows the PhD of Antoine Tonnoir (now Assistant Professor at Insa of Rouen) who developed a new approach, the Half-Space Matching Method, to solve scattering problems in 2D unbounded anisotropic media. The objective is to extend the method to a 3D plate of finite width.

In 2D, our approach consists in coupling several plane-waves representations of the solution in half-spaces surrounding the defect with a FE computation of the solution around the defect. The difficulty is to ensure that all these representations match, in particular in the infinite intersections of the half-spaces. It leads to a formulation which couples, via integral operators, the solution in a bounded domain including the defect and some traces of the solution on the edges of the half-planes. We have proven that, in presence of dissipation, this system is a Fredholm equation of the second kind, in an L2 functional framework. The truncation of the Fourier integrals and the finite element approximation of the corresponding numerical method have been also analyzed.

The method has been extended to the 3D case, for an application to non-destructive testing. The objective is to simulate the interaction of Lamb waves with a defect in an anisotropic elastic plate. The additional complexity compared to the 2D case lies in the representations which are obtained semi-analytically by decomposition on Lamb modes. In addition, the system of equations couples the FE representation in the bounded perturbed domain with not only the displacement, but also the normal stress of the solution on the infinite bands limiting the half-plates. A first numerical result has been obtained in the isotropic case.

The perspectives now concern the efficiency of the method (which could be improved by replacing the direct inversion by a preconditioned iterative inversion with an efficient product matrix-vector), the analysis of the method in the case without dissipation and the analysis of the method in the elastic case.

Coupling BEMs in overlapping domains when a global Green’s function is not available

Participants : Anne-Sophie Bonnet Ben-Dhia, Stéphanie Chaillat, Sonia Fliss, Yohanes Tjandrawidjaja.

We consider in this work problems for which the Green’s function is not available, so that classical Boundary Integral equation methods are not applicable. Let us mention for instance the junction of two different stratified media (tapered optical fibers in integrated optics or junction of two topographic elastic surfaces in geophysics).

To this end, we propose a generalization of the Half-Space Matching method (see section 7.3.1).

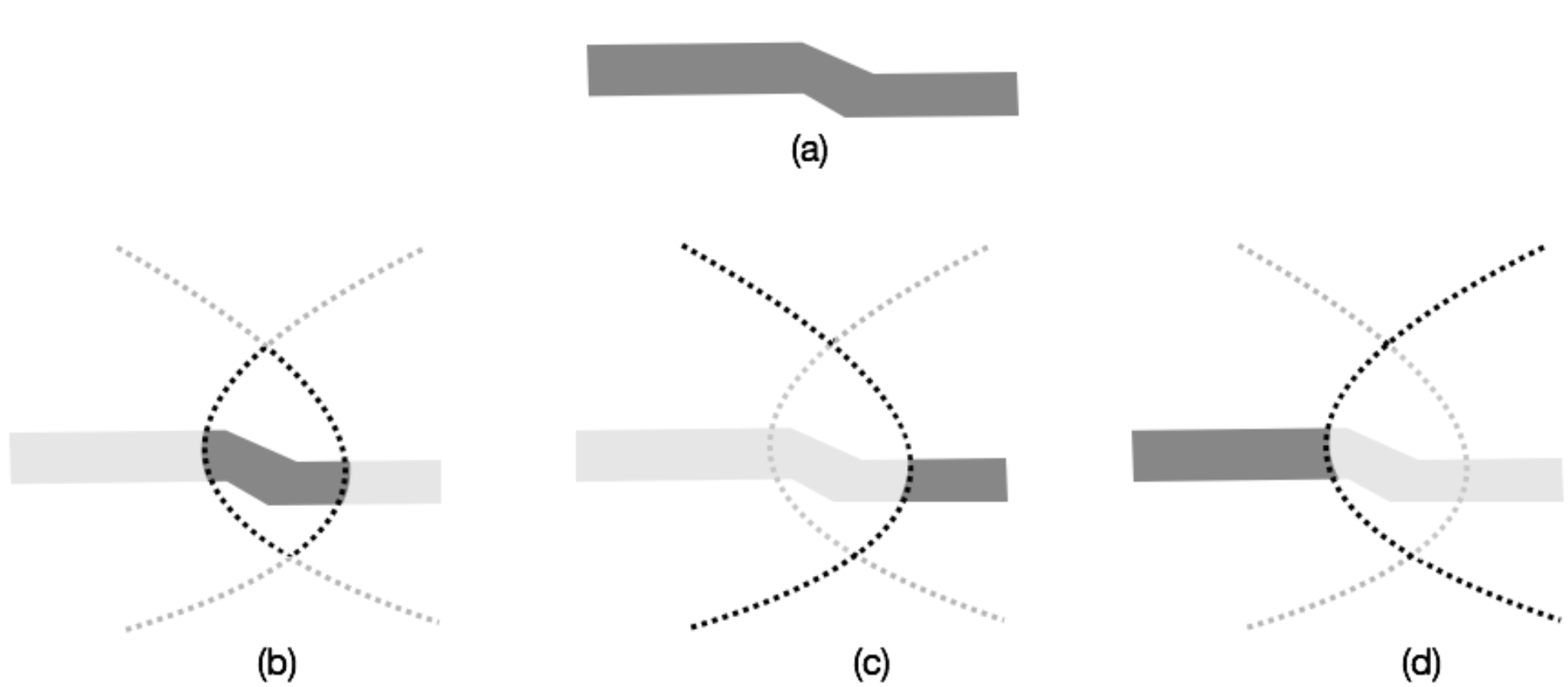
In this work, by replacing the Fourier representations by integral representations, we are able to replace the half-spaces by more general unbounded overlapping sub-domains. We choose the sub-domains in such a way that an explicit Green’s function is available for each subdomain. For instance, for the configuration described above (figure 1a), it suffices to introduce two infinite sub domains, each of them containing only one stratification (figures 1c and 1d) and a bounded domain containing the junction (figure 1b). The formulation couples the solution in the bounded domain with the single and double layer potentials on each boundary of the sub-domains. The approximation relies on a FE discretisation of the volume unknown and a truncation and a discretization of the boundary/surface unknowns.

A study concerning the choice of the discretisation parameters and the shape of the infinite lines have to be done. The theoretical analysis of the method raises challenging open questions: for instance, a first uniqueness result has been derived, which requires the definition of a variational formulation on a Rie. Finally, we want to apply the method to the scattering by a step, i.e. the junction of two semi infinite-planes joined together by a step.

Domain decomposition method for acoustics with uniform exponential rate of convergence using non-local impedance operators

Participants : Patrick Joly, Francis Collino, Émile Parolin.

This work is done in the framework of the PhD of Émile Parolin (funded by ANR NonlocalDD), in collaboration with X. Clayes (EPI Alpines & LJLL).

We continued the work on non-overlapping domain decomposition methods with non-local transmission conditions for time-harmonic wave propagation. The analysis of such methods is conducted by writing them as a relaxed Jacobi algorithm. In the absence of junctions points, the continuous algorithm converges exponentially fast under suitable assumptions on the impedance operators. These assumptions cannot be satisfied using local operators and rely in practice on singular integral operators. The progress achieved is as follows.

• In the context of acoustic wave propagation, we established a new result on the robustness of the algorithm with respect to the mesh size. We have proven that for Lagrange finite element approximations the exponential rate of convergence of the algorithm is independent of the discretization parameter, hence does not deteriorate when the mesh is refined. The proof relies on the Scott-Zhang interpolator and led to the submission.

• We have been working on the extension to 3D time harmonic Maxwell's equations. The main difficulty is to design well adapted operators taking into account the specificity of the corresponding trace spaces. An adequate operator must behave like a pseudo-differential operator with opposite order on the `curl part' and `grad part' of a tangential field (this is related to the Helmholtz decomposition of tangential fields). Guided by potential theory for elliptic operators, we proposed two classes of suitable operators. The first one is based on Bessel potentials (fractional powers of the shifted Laplacian) and the second one relies on Riesz potentials. We have shown that the proposed operators satisfy the desired properties in the case of a sphere using modal analysis techniques. We have also been working on the design of the finite element approximation of these operators.

Domain decomposition method with cross-point treatment for high-frequency acoustic scattering

Participant : Axel Modave.

This work is done in collaboration with X. Antoine (IECL & EPI SPHINX) and C. Geuzaine (Université de Liège).

Solving high-frequency time-harmonic scattering problems using FE techniques is challenging, as such problems lead to very large, complex and indefinite linear systems. Optimized Schwarz domain decomposition methods (DDMs) are currently a very promising approach, where subproblems of smaller sizes are solved in parallel using direct solvers, and are combined in an iterative procedure. It is well-known that the convergence rate of these methods strongly depends on the transmission condition enforced on the interfaces between the subdomains.

Local transmission conditions based on high-order absorbing boundary conditions (HABCs) have proved well suited. They represent a good compromise between basic impedance conditions (which lead to suboptimal convergence) and the exact Dirichlet-to-Neumann (DtN) map related to the complementary of the subdomain (which is expensive to compute). However, a direct application of this approach for domain decomposition configurations with cross-points, where more than two subdomains meet, does not provide satisfactory results.

We work on improved DDMs that efficiently addresses configurations with cross-points. Noting that these points actually are corners for the subdomains, our strategy consists in incorporating a corner treatment developed for HABCs (see section 7.7.1) into the DDM procedure. We propose a cross-point treatment for HABC-based DDMs in settings with cross-points and right angles. The method is implemented and successfully tested for two-dimensional examples. The analysis of this method is currently in progress. Extensions to more complicated settings (e.g. 3D, with non-right angles, other physical waves) will be investigated in the future.