Section: New Results

Approximation

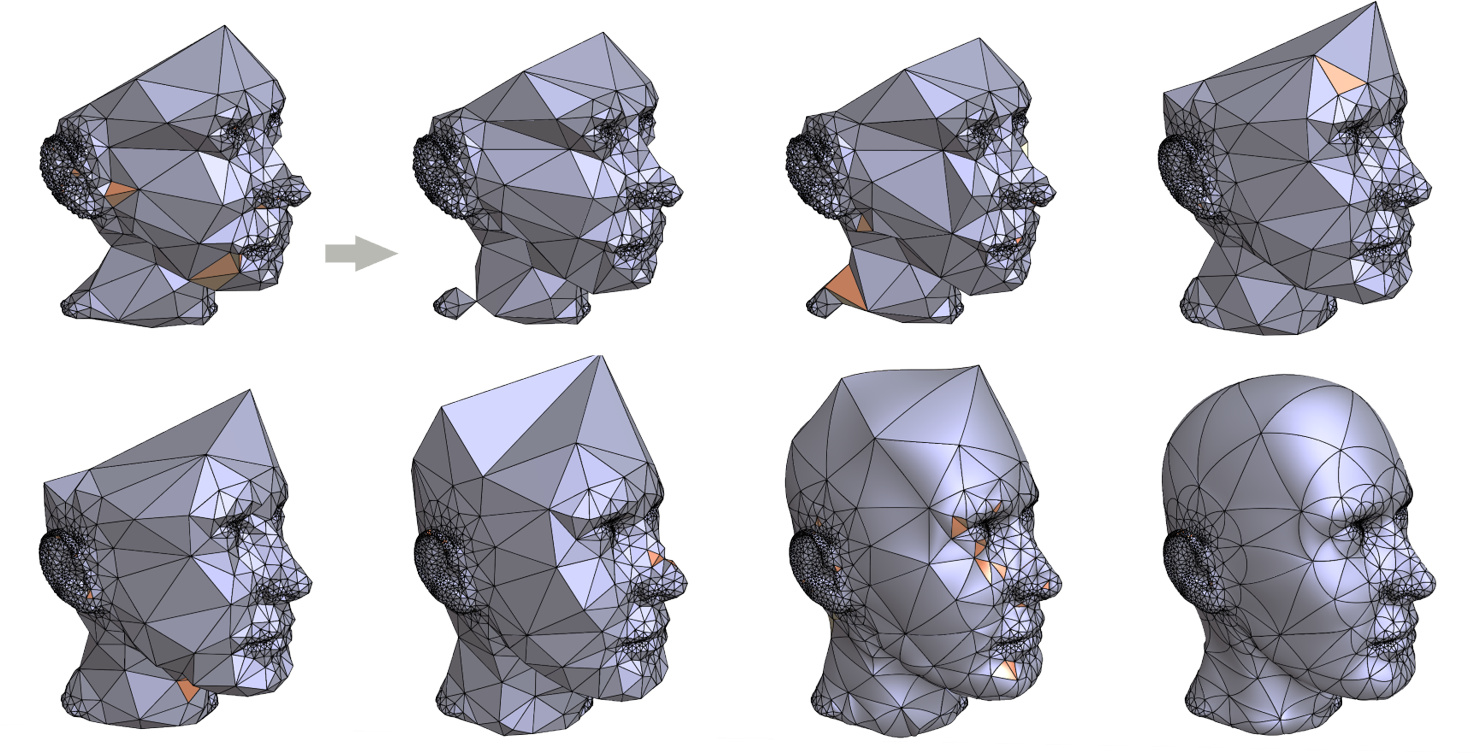
Curved Optimal Delaunay Triangulation

Participants : Mathieu Desbrun, Pierre Alliez [contact] .

Work in collaboration with Leman Feng (Ecole des Ponts ParisTech), Hervé Delingette (EPIONE) and Laurent Busé (AROMATH).

Higher-order meshing, Optimal Delaunay Triangulations, higher order finite elements, Bézier elements.

Meshes with curvilinear elements hold the appealing promise of enhanced geometric flexibility and higher-order numerical accuracy compared to their commonly-used straight-edge counterparts. However, the generation of curved meshes remains a computationally expensive endeavor with current meshing approaches: high-order parametric elements are notoriously difficult to conform to a given boundary geometry, and enforcing a smooth and non-degenerate Jacobian everywhere brings additional numerical difficulties to the meshing of complex domains. In this paper, we propose an extension of Optimal Delaunay Triangulations (ODT) to curved and graded isotropic meshes. By exploiting a continuum mechanics interpretation of ODT instead of the usual approximation theoretical foundations, we formulate a very robust geometry and topology optimization of Bézier meshes based on a new simple functional promoting isotropic and uniform Jacobians throughout the domain. We demonstrate that our resulting curved meshes can adapt to complex domains with high precision even for a small count of elements thanks to the added flexibility afforded by more control points and higher order basis functions (see Figure 9). This work has been published in the proceedings of ACM SIGGRAPH conference [12].