Section: New Results

Reconstruction

Kinetic Polygonal Partitioning of Images

Participants : Jean-Philippe Bauchet, Florent Lafarge [contact] .

Polygons, image segmentation, object contouring, kinetic framework

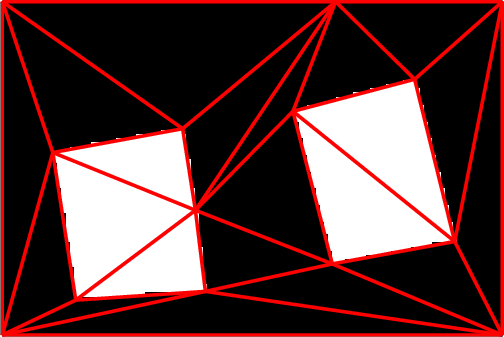
Recent works showed that floating polygons can be an interesting alternative to traditional superpixels, especially for analyzing scenes with strong geometric signatures, as man-made environments. Existing algorithms produce homogeneously-sized polygons that fail to capture thin geometric structures and over-partition large uniform areas. We propose a kinetic approach that brings more flexibility on polygon shape and size. The key idea consists in progressively extending pre-detected line-segments until they meet each other. Our experiments demonstrate that output partitions both contain less polygons and better capture geometric structures than those delivered by existing methods. We also show the applicative potential of the method when used as preprocessing in object contouring. Figure 6 illustrates the goal of our method. This work has been published in the proceedings of CVPR [15].

Polygonization of Binary Classification Maps Using Mesh Approximation with Right Angle Regularity

Participants : Onur Tasar, Pierre Alliez, Yuliya Tarabalka [contact] .

Work in collaboration with Emmanuel Maggiori.

Polygonization, vectorization, remote sensing, classification maps, mesh approximation, right angles

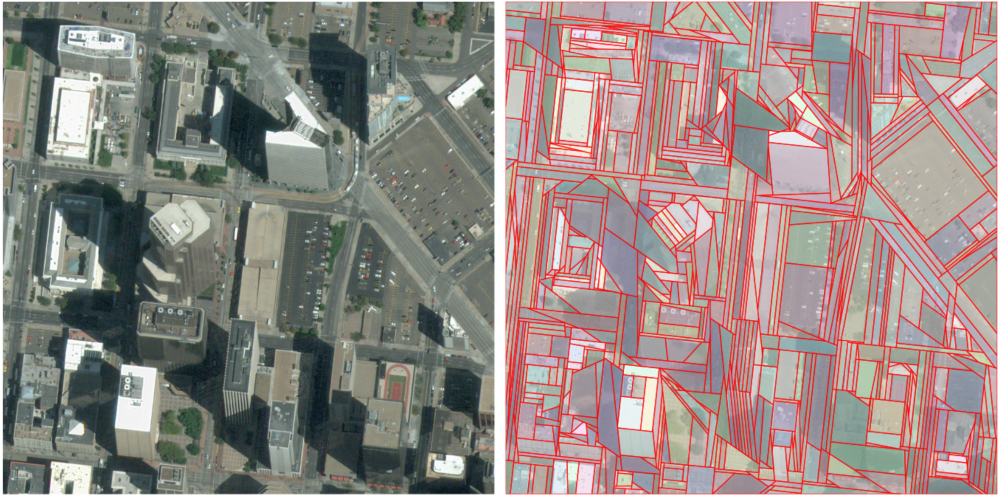
One of the most popular and challenging tasks in remote sensing applications is the generation of digitized representations of Earth's objects from satellite raster image data. A common approach to tackle this challenge is a two-step method that first involves performing a pixel-wise classification of the raster data, then vectorizing the obtained classification map. We propose a novel approach, which recasts the polygonization problem as a mesh-based approximation of the input classification map, where binary labels are assigned to the mesh triangles to represent the building class. A dense initial mesh is decimated and optimized using local edge and vertex-based operators in order to minimize an objective function that models a balance between fidelity to the classification map in ${\ell }_1$ norm sense, right angle regularity for polygonized buildings, and final mesh complexity (see Fig. 7). Experiments show that adding the right angle objective yields better representations quantitatively and qualitatively than previous work and commonly used polygon generalization methods in remote sensing literature for similar number of vertices. This work was published at IGARSS [19].

End-to-End Learning of Polygons for Remote Sensing Image Classification

Participants : Nicolas Girard, Yuliya Tarabalka [contact] .

High-resolution aerial images, polygon, vectorial, regression, deep learning, convolutional neural networks

While geographic information systems typically use polygonal representations to map Earth's objects, most state-of-the-art methods produce maps by performing pixelwise classification of remote sensing images, then vectorizing the outputs. This work studies if one can learn to directly output a vectorial semantic labeling of the image. We here cast a mapping problem as a polygon prediction task, and propose a deep learning approach which predicts vertices of the polygons outlining objects of interest. Experimental results on the Solar photovoltaic array location dataset show that the proposed network succeeds in learning to regress polygon coordinates, yielding directly vectorial map outputs (see Fig. 8). This work has been published in the proceedings of IGARSS [14].