Section: Research Program

Marine and coastal systems

Multi-scale ocean modelling

The expertise of LEMON in this scientific domain is more in the introduction and analysis of new boundary conditions for ocean modelling systems, that can be tested on academical home-designed test cases. This is in the core of Antoine Rousseau's contributions over the past years. The real implementation, within operational ocean models, has to be done thanks to external collaborations which have already started with LEMON (see below).

State of the Art

In physical oceanography, all operational models - regardless of the scale they apply to - are derived from the complete equations of geophysical fluid dynamics. Depending on the considered process properties (nonlinearity, scale) and the available computational power, the original equations are adapted with some simplifying hypotheses. The reader can refer to [58], [51] for a hierarchical presentation of such models.

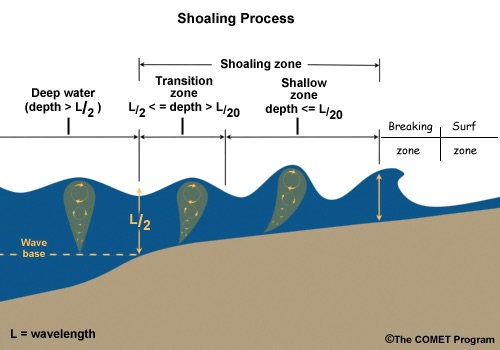
In the nearshore area, the hydrostatic approximation that is used is most large scales models (high sea) cannot be used without a massive loss of accuracy. In particular, shallow water models are inappropriate to describe the physical processes that occur in this zone (see Figure 1). This is why Boussinesq-type models are prefered: see [49]. They embed dispersive terms that allow for shoaling and other bathymetry effects. Since the pioneering works of Green and Naghdi (see [36]), numerous theoretical and numerical studies have been delivered by the "mathematical oceanography" community, more specifically in France (see the works of Lannes, Marche, Sainte-Marie, Bresch, etc.). The corresponding numerical models (BOSZ, WaveBox) must thus be integrated in any reasonable nearshore modelling platform.

However, these models cannot simply replace all previous models everywhere in the ocean: dispersive models are useless away from the shore and it is known that wave breaking cannot be simulated using Boussinesq-type equations. Hence the need to couple these models with others. Some work has been done in this direction with a multi-level nesting using software packages such as ROMS, but to the best of our knowledge, all the "boxes" rely on the same governing equations with different grid resolutions. A real coupling between different models is a more difficult task since different models may have different mathematical properties, as shown in the work by Eric Blayo and Antoine Rousseau on shallow water modelling (see [17]).

Four year research objectives

Starting from the knowledge acquired in the collaboration with Eric Blayo on model coupling using domain decomposition techniques, our ambition is to propose theoretical and numerical tools in order to incorporate nearshore ocean models into large complex systems including several space and time scales. Two complementary research directions are considered:

• Dispersive vs non-dispersive shallow water models. As depicted in Figure 1 above, Boussinesq-type models (embedding dispersive effects) should be used in the so-called shoaling zone. The coupling with classical deep-sea / shallow water models has to be done such that all the processes in Figure 1 are correctly modelled (by different equations), with a reduced numerical cost. As a first guess, we think that Schwarz-type methods (widely used by the DDM community) could be good candidates, in particular when the interface locations are well-known. Moving interfaces (depending on the flow, the bathymetry and naturally the wind and all external forcings) is a more challenging objective that will be tackled after the first step (known interface) is achieved.

• spectral vs time-domain models. In the context of mathematical modelling and numerical simulation for the marine energy, we want to build a coupled numerical model that would be able to simulate wave propagation in domains covering both off-shore regions, where spectral models are used, and nearshore regions, better described by nonlinear dispersive (Boussinesq-type) models.

  While spectral models work with a statistical and phase-averaged description of the waves, solving the evolution of its energy spectrum, Boussinesq-type models are phase-resolving and solves nonlinear dispersive shallow water equations for physical variables (surface elevation and velocity) in the time domain. Furthermore, the time and space scales are very different: they are much larger in the case of spectral models, which justifies their use for modelling off-shore propagation over large time frames. Moreover, important small scale phenomena in nearshore areas are better captured by Boussinesq models, in which the time step is limited by the CFL condition.

  From a mathematical and modelling point of view, this task mainly consists in working on the boundary conditions of each model, managing the simultaneous use of spectral and time series data, while studying transparent boundary conditions for the models and developing domain decomposition approaches to improve the exchange of information.

People

Antoine Rousseau, Joao Guilherme Caldas Steinstraesser

External collaborations

• Eric Blayo is the former scientific leader of team MOISE in Grenoble, where Antoine Rousseau was first recruited. Eric Blayo and Antoine Rousseau have co-advised 3 PhDs and continue to work together on coupling methods in hydrodynamics, especially in the framework of the COMODO ANR network.

• Fabien Marche (at IMAG, Montpellier, currently on leave in Bordeaux) is an expert in numerical modelling and analysis of Boussinesq-type models. He is the principal investigator of the WaveBox software project, to be embedded in the national scale Uhaina initiative.

• In the framework of its collaboration with MERIC, Antoine Rousseau and Joao Guilherme Caldas Steinstraesser collaborate with the consortium DiMe (ANR-FEM project), and more particularly with Jean-François Filipot ans Volker Roeber for the coupling of spectral and time-domain methods.

Data-model interactions

State of the Art

An alternative to direct observations is the chaining of numerical models, which for instance represent the physic from offshore to coastal areas. Typically, output data from atmospheric and ocean circulation models are used as forcings for a wave model, which in turn feeds a littoral model. In the case of extreme events, their numerical simulation from physical models is generally unreachable. This is due to a lack of knowledge on boundary conditions and on their physical reliability for such extreme quantities. Based on numerical simulated data, an alternative is to use statistical approaches. [21] proposed such an approach. They first produced and studied a 52-year hindcast using the WW3 wave model [19], [22], [20], [66]. Then stemming from parts of the original work of [18], [37], [32], [21] proposed a semi-parametric approach which aims to simulate extreme space-time waves processes to, in turn, force a littoral hazard model. Nevertheless their approach allows only a very small number of scenarii to be simulated.

Four year research objectives

A first objective is to establish the link between the simulation approach proposed by [21] and the Pareto Processes [32]. This will allow the work of [21] to be generalized, thus opening up the possibility of generating an infinity of extreme scenarii. While continuing to favor the semi- or non-parametric approaches made possible by the access to high spatial resolution calculations, we will try to capture the strength of potentially decreasing extremal dependence when moving towards higher values, which requires the development of models that allow for so-called asymptotic independence.

People

Gwladys Toulemonde, Fátima Palacios Rodríguez, Antoine Rousseau

External collaborations

• since late 2019, LEMON has started a collaboration with IRT Saint-Exupéry on the hybridization of models and large amounts of data for the modelling of urban floods

• The collaboration with Romain Chailan (IMAG, UM, CNRS) and Frédéric Bouchette (Geosciences, UM) started in 2012 during the PhD of Romain entitled Application of scientific computing and statistical analysis to address coastal hazards.

• During her post doctoral position, Fátima Palacios Rodríguez with her co-advisors will considered a generalization of the proposed simulation method by [21].