Section: New Results

Statistical Machine Learning

A Contextual Bandit Bake-off

Participants : Alberto Bietti, Alekh Agarwal [Microsoft Research] , John Langford [Microsoft Research] .

Contextual bandit algorithms are essential for solving many real-world interactive machine learning problems. Despite multiple recent successes on statistically and computationally efficient methods, the practical behavior of these algorithms is still poorly understood. In , we leverage the availability of large numbers of supervised learning datasets to compare and empirically optimize contextual bandit algorithms, focusing on practical methods that learn by relying on optimization oracles from supervised learning. We find that a recent method using optimism under uncertainty works the best overall. A surprisingly close second is a simple greedy baseline that only explores implicitly through the diversity of contexts, followed by a variant of Online Cover which tends to be more conservative but robust to problem specification by design. Along the way, we also evaluate and improve several internal components of contextual bandit algorithm design. Overall, this is a thorough study and review of contextual bandit methodology.

A Generic Acceleration Framework for Stochastic Composite Optimization

Participants : Andrei Kulunchakov, Julien Mairal.

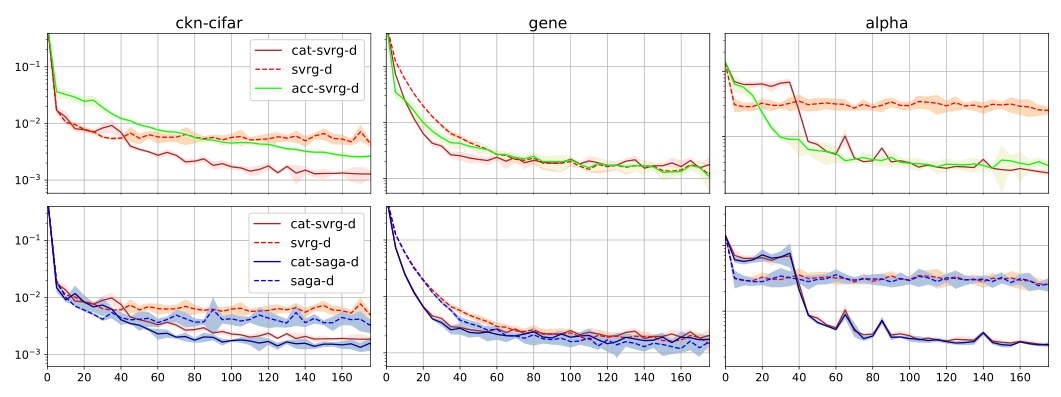
In [35], we introduce various mechanisms to obtain accelerated first-order stochasticoptimization algorithms when the objective function is convex or stronglyconvex. Specifically, we extend the Catalyst approach originally designed fordeterministic objectives to the stochastic setting. Given an optimizationmethod with mild convergence guarantees for strongly convex problems,the challenge is to accelerate convergence to a noise-dominated region, andthen achieve convergence with an optimal worst-case complexity depending on thenoise variance of the gradients.A side contribution of our work is also a generic analysis that canhandle inexact proximal operators, providing new insights about the robustness of stochastic algorithms when the proximal operator cannot be exactly computed. An illustration from this work is explained in Figure 12.

Estimate Sequences for Variance-Reduced Stochastic Composite Optimization

Participants : Andrei Kulunchakov, Julien Mairal.

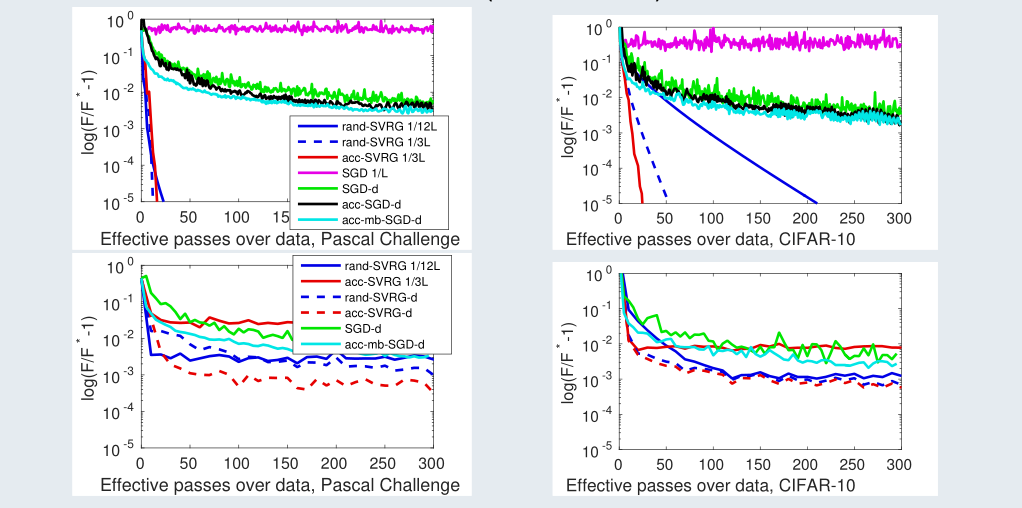
In [23], we propose a unified view of gradient-based algorithms for stochastic convex composite optimization. By extending the concept of estimate sequence introduced by Nesterov, we interpret a large class of stochastic optimization methods as procedures that iteratively minimize a surrogate of the objective. This point of view covers stochastic gradient descent (SGD), the variance-reduction approaches SAGA, SVRG, MISO, their proximal variants, and has several advantages: (i) we provide a simple generic proof of convergence for all of the aforementioned methods; (ii) we naturally obtain new algorithms with the same guarantees; (iii) we derive generic strategies to make these algorithms robust to stochastic noise, which is useful when data is corrupted by small random perturbations. Finally, we show that this viewpoint is useful to obtain accelerated algorithms. A comparison with different approaches is shown in Figure 13.

White-box vs Black-box: Bayes Optimal Strategies for Membership Inference

Participants : Alexandre Sablayrolles, Matthijs Douze, Yann Ollivier, Cordelia Schmid, Hervé Jégou.

Membership inference determines, given a sample and trained parameters of a machine learning model, whether the sample was part of the training set. In this paper [28], we derive the optimal strategy for membership inference with a few assumptions on the distribution of the parameters. We show that optimal attacks only depend on the loss function, and thus black-box attacks are as good as white-box attacks. As the optimal strategy is not tractable, we provide approximations of it leading to several inference methods 14, and show that existing membership inference methods are coarser approximations of this optimal strategy. Our membership attacks outperform the state of the art in various settings, ranging from a simple logistic regression to more complex architectures and datasets, such as ResNet-101 and Imagenet.