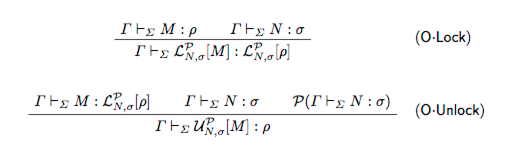Accessibility setting

Section: New Results

An Open Logical Framework

Participants : Luigi Liquori [contact] , Marina Lenisa [Univ. Udine] , Furio Honsell [Univ. Udine] , Petar Maksimovic, Ivan Scagnetto [Univ. Udine] .

The LFP Framework is an extension of the Harper-Honsell-Plotkin's Edinburgh Logical Framework LF with external predicates, hence the name Open Logical Framework. This is accomplished by defining lock type constructors, which are a sort of “diamond”-modality constructors, releasing their argument under the condition that a possibly external predicate is satisfied on an appropriate typed judgement. Lock types are defined using the standard pattern of constructive type theory, i.e. via introduction, elimination, and equality rules. Using LFP, one can factor out the complexity of encoding specific features of logical systems which would otherwise be awkwardly encoded in LF, e.g. side-conditions in the application of rules in Modal Logics, and sub-structural rules, as in non-commutative Linear Logic. The idea of LFP is that these conditions need only to be specified, while their verification can be delegated to an external proof engine, in the style of the Poincaré Principle or Deduction Modulo. Indeed such paradigms can be adequately formalized in LFP. We investigate and characterize the meta-theoretical properties of the calculus underpinning LFP: strong normalization, confluence, and subject reduction. This latter property holds under the assumption that the predicates are well-behaved, i.e. closed under weakening, permutation, substitution, and reduction in the arguments. Moreover, we provide a canonical presentation of LFP, based on a suitable extension of the notion of $\beta \eta$-long normal form, allowing for smooth formulations of adequacy statements.

LFP is parametric over a potentially unlimited set of (well-behaved) predicates P, which are defined on derivable typing judgements of the form $\Gamma {⊢}_{\Sigma }N:\sigma$, see Fig 13 .

Figure 13. Some rule of the Open Logical Framework

The syntax of LFP predicates is not specified, with the main idea being that their truth is to be verified via a call to an external validation tool; one can view this externalization as an oracle call. Thus, LFP allows for the invocation of external “modules” which, in principle, can be executed elsewhere, and whose successful verification can be acknowledged in the system via L-reduction. Pragmatically, lock types allow for the factoring out of the complexity of derivations by delegating the {checking, verification, computation} of such predicates to an external proof engine or tool. The proof terms themselves do not contain explicit evidence for external predicates, but just record that a verification {has to be (lock), has been successfully (unlock)} carried out. In this manner, we combine the reliability of formal proof systems based on constructive type theory with the efficiency of other computer tools, in the style of the Poincaré Principle. In this paper, we develop the meta-theory of LFP. Strong normalization and confluence are proven without any additional assumptions on predicates. For subject reduction, we require the predicates to be well-behaved, i.e. closed under weakening, permutation, substitution, and $\beta ℒ$-reduction in the arguments. LFP is decidable, if the external predicates are decidable. We also provide a canonical presentation of LFP, based on a suitable extension of the notion of $\beta \eta$-long normal form. This allows for simple proofs of adequacy of the encodings. In particular, we encode in LFP the call-by-value $\lambda$-calculus and discuss a possible extension which supports the design-by-contract paradigm. We provide smooth encodings of side conditions in the rules of Modal Logics, both in Hilbert and Natural Deduction styles. We also encode sub-structural logics, i.e. non-commutative Linear Logic. We also illustrate how LFP can naturally support program correctness systems and Hoare-like logics. In our encodings, we utilize a library of external predicates. As far as expressiveness is concerned, LFP is a stepping stone towards a general theory of shallow vs deep encodings, with our encodings being shallow by definition. Clearly, by Church's thesis, all external decidable predicates in LFP can be encoded, possibly with very deep encodings, in standard LF. It would be interesting to state in a precise categorical setting the relationship between such deep internal encodings and the encodings in LFP. LFP can also be viewed as a neat methodology for separating the logical-deductive contents from, on one hand, the verification of structural and syntactical properties, which are often needlessly cumbersome but ultimately computable, or, on the other hand, from more general means of validation.