Section: New Results

Analysis

Detecting Parametric Objects in Large Scenes by Monte Carlo Sampling

Participants : Yannick Verdie, Florent Lafarge.

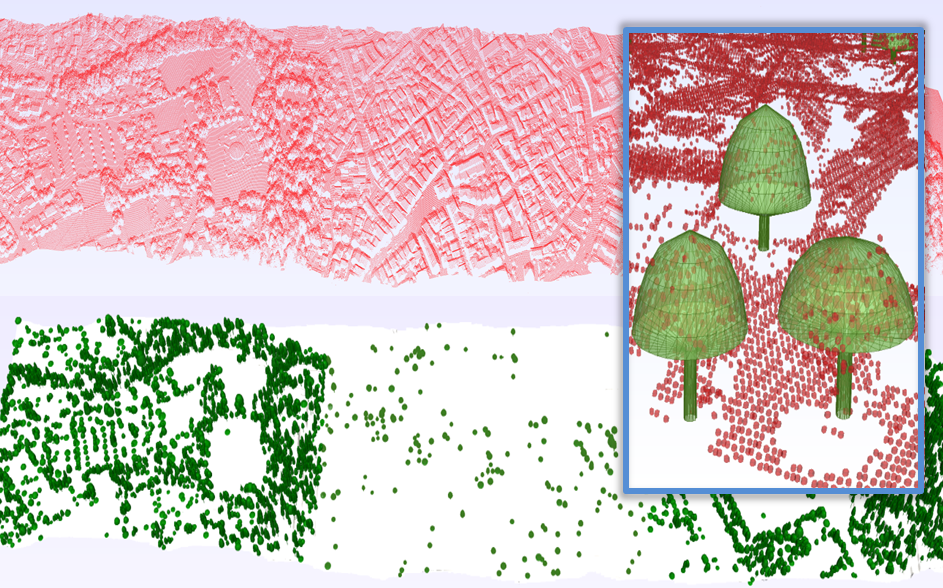
Point processes constitute a natural extension of Markov Random Fields (MRF), designed to handle parametric objects. They have shown efficiency and competitiveness for tackling object extraction problems in vision. Simulating these stochastic models is however a difficult task. The performance of existing samplers are limited in terms of computation time and convergence stability, especially on large scenes. We propose a new sampling procedure based on a Monte Carlo formalism [11] . Our algorithm exploits the Markovian property of point processes to perform the sampling in parallel. This procedure is embedded into a data-driven mechanism so that the points are distributed in the scene as a function of spatial information extracted from the input data. The performance of the sampler is analyzed through a set of experiments on various object detection problems from large scenes, including comparisons to the existing algorithms. The sampler is also evaluated as an optimization algorithm for MRF-based labeling problems (Figure 1 ).

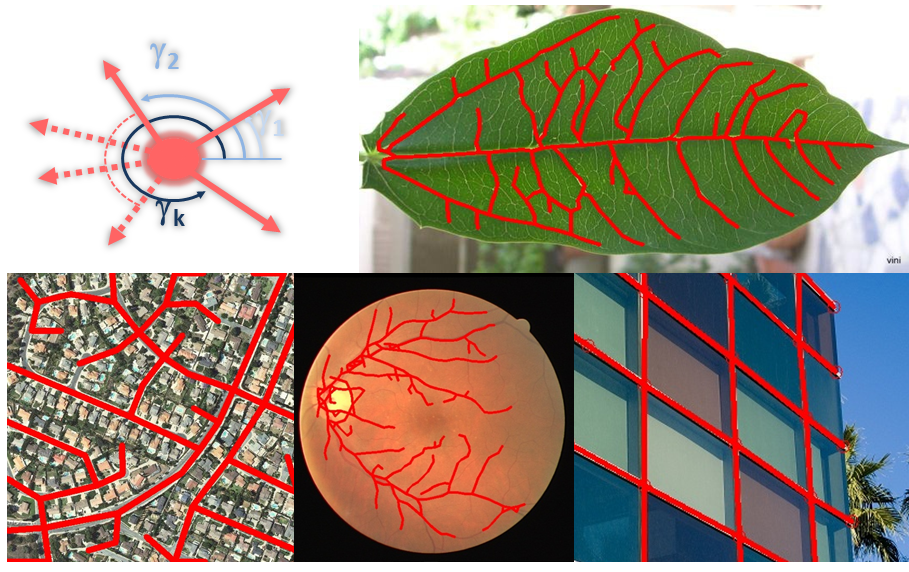
Recovering Line-networks in Images by Junction-Point Processes

Participant : Florent Lafarge.

In collaboration with Dengfeng Chai (Zheijiang University, China) and Wolfgang Forstner (University of Bonn, Germany).

We tackle the automatic extraction of line-networks from images. Appearance and shape considerations have been deeply explored in the literature to improve accuracy in presence of occlusions, shadows, and a wide variety of irrelevant objects. However most existing work has ignored the structural aspect of the problem. We present an original method which provides structurally-coherent solutions [13] . Contrary to the pixel-based and object-based methods, our result is a graph in which each node represents either a connection or an ending in the line-network. Based on stochastic geometry, we develop a new family of point processes consisting in sampling junction-points in the input image by using a Monte Carlo mechanism. The quality of a configuration is measured by a probability density which takes into account both image consistency and shape priors. Our experiments on a variety of problems illustrate the potential of our approach in terms of accuracy, flexibility and efficiency (Figure 2 ).