Section: New Results

Approximation

Integer-Grid Maps for Reliable Quad Meshing

Participants : David Bommes, Pierre Alliez.

In collaboration with Leif Kobbelt from RWTH Aachen.

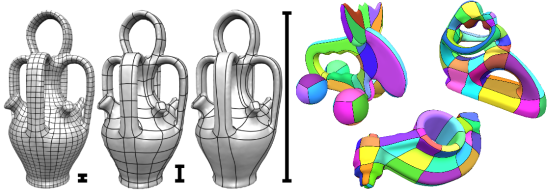
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties. Two of those are (1) high regularity due to explicit control over irregular vertices and (2) smooth distribution of distortion achieved by convex variational formulations. In this work [2] we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP we propose two additional optimizations: a complexity reduction algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space from the input complexity of the triangle mesh, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers. Our algorithm also enables the global search for high-quality coarse quad layouts as illustrated in Figure 3 , a difficult task solely tackled by insufficient greedy methodologies before.

QEx: Robust Quad Mesh Extraction

Participant : David Bommes.

In collaboration with Leif Kobbelt from RWTH Aachen.

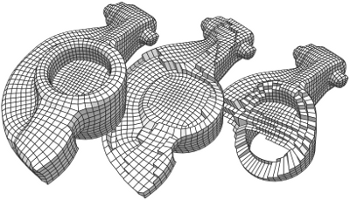
Among the class of quad remeshing techniques, the ones based on parameterization strive to generate an integer-grid map, i.e., a parametrization of the input surface in 2D such that the canonical grid of integer iso-lines forms a quad mesh when mapped back onto the surface in 3D. An essential, albeit broadly neglected aspect of these methods is the quad extraction step. This step is not a trivial matter: ambiguities induced by numerical inaccuracies and limited solver precision, as well as imperfections in the maps produced by most methods (unless costly countermeasures are taken) pose significant hurdles to the quad extractor. In this work [6] we present a method to sanitize a provided parametrization such that it becomes numerically consistent even with limited precision floating point arithmetic. We also devise a novel strategy to cope with common local fold-overs in the parametrization. We can generate all-quadrilateral meshes where otherwise holes, non-quad polygons or no output at all would have been produced like for the example in Figure 4 .

Advanced Automatic Hexahedral Mesh Generation from Surface Quad Meshes

Participant : David Bommes.

In collaboration with Leif Kobbelt (RWTH Aachen).

A purely topological approach for the generation of hexahedral meshes from quadrilateral surface meshes of genus zero has been proposed by M. Müller-Hannemann: in a first stage, the input surface mesh is reduced to a single hexahedron by successively eliminating loops from the dual graph of the quad mesh; in the second stage, the hexahedral mesh is constructed by extruding a layer of hexahedra for each dual loop from the first stage in reverse elimination order. We introduce several techniques to extend the scope of target shapes of the approach and significantly improve the quality of the generated hexahedral meshes [14] . While the original method can only handle almost-convex objects and requires mesh surgery and remeshing in case of concave geometry, we propose a method to overcome this issue by introducing the notion of concave dual loops in order to handle non-convex objects like the one displayed in Figure 5 . Furthermore, we analyze and improve the heuristic to determine the elimination order for the dual loops such that the inordinate introduction of interior singular edges, i.e., edges of degree other than four in the hexahedral mesh, can be avoided in many cases.

On the Equilibrium of Simplicial Masonry Structures

Participant : Pierre Alliez.

In collaboration with Mathieu Desbrun, Fernando de Goes and Houman Owhadi from Caltech.

We contributed a novel approach for the analysis and design of self-supporting simplicial masonry structures [4] . A finite-dimensional formulation of their compressive stress field is derived, offering a new interpretation of thrust networks through numerical homogenization theory. We further leverage geometric properties of the resulting force diagram to identify a set of reduced coordinates characterizing the equilibrium of simplicial masonry. We finally derive computational form-finding tools that improve over previous work in efficiency, accuracy, and scalability.