Section: New Results

A well-balanced and positive preserving DG scheme for the SW equations

Participants : Arnaud Duran, Fabien Marche.

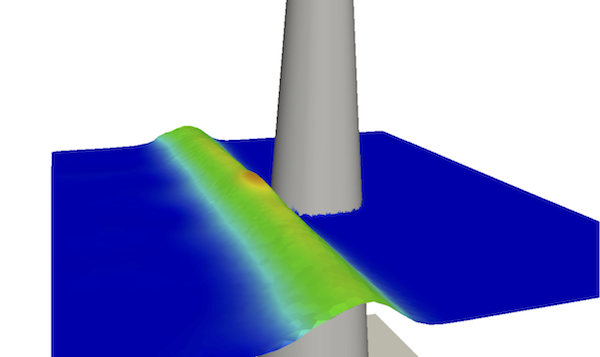
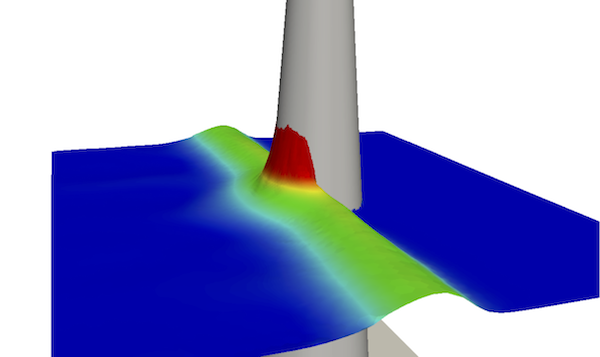
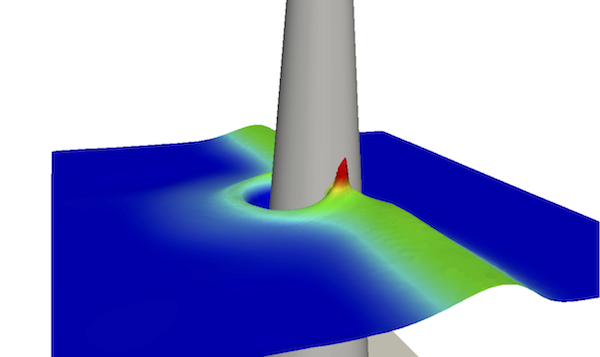
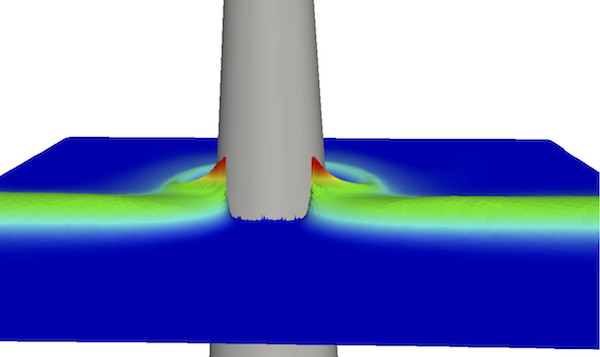
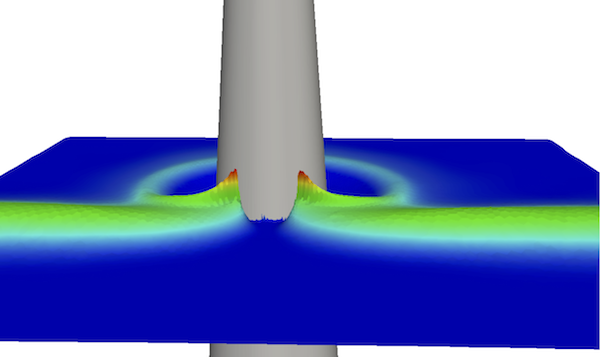
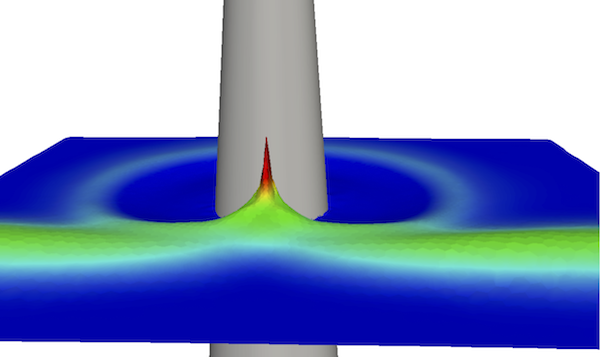
We consider in [5] the discontinuous Galerkin discretization of the nonlinear Shallow Water equations on unstructured triangulations. We propose an efficient combination of ingredients that leads to a simple high-order robust and well-balanced scheme, based on the alternative formulation of the equations known as the pre-balanced shallow water equations. We show that the preservation of the motionless steady states can be achieved, for an arbitrary order of polynomial expansion. Additionally, the preservation of the positivity of the water height is ensured using the recent method introduced in [59] . Some comparisons with a recent finite-volume MUSCL approach are also performed. The well-known tsunami test case shown in figures 6 and 7 has been computed here with high order DG scheme on unstructured triangulation.

Figure 6. Tsunami wave over a conical island - Lateral view of the free surface at times t=5,6 and 7s.

Figure 7. Tsunami wave over a conical island - Rear view of the free surface at times t=8,9 and 10s.